Мозголин Андрей Сергеевич

выпускник Костромского Государственного Университета имени Н.А. Некрасова.

Неоднородный рациональный Б-сплайн, NURBS (от англ. Non-uniform rational B-spline) – математическая модель, применяемая для генерации и представления кривых и поверхностей [13]. NURBS является наиболее простым и универсальным способом задания кривых и поверхностей любой сложности.

Сначала мы рассмотрим математическую модель, описывающую построение NURBS кривых, а затем перейдем к NURBS поверхностям.

Полиномиальные параметрические кривые

В компьютерной графике широко применяется метод построения кривых по контрольным точкам, т.е. по некоторой ломаной кривой строится гладкая кривая. Данный метод получил широкое распространение благодаря своей простоте и универсальности. Меняя положение контрольных точек, мы можем менять вид кривой. Общий вид формулы, описывающей кривую в параметрической форме [1]:

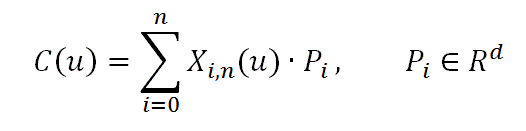
Функция X[i,n](u)  называется базисной функцией и представляет собой полином n – ой степени, P[i] – управляющие коэффициенты, при изменении которых меняется вид кривой. Наиболее широко известными видами базисных функций являются:

- полином Лагранжа;

- полином Бернштейна;

- базисная функция Б-сплайна;

Как видно из названия, именно базисная функция Б-сплайна является основой для NURBS кривых и поверхностей, ее мы и будем рассматривать.

Базисная функция Б-сплайна

Пусть U = {u[0], u[1] ..., u[m] }  неубывающая последовательность действительных чисел, т.е. u[i] <= u[i+1] i=0,.m-1. Где u[i]  называются узлами, а U узловым вектором. Тогда i-той базисной функцией Б-сплайна степени  является следующая рекурсивная функция:

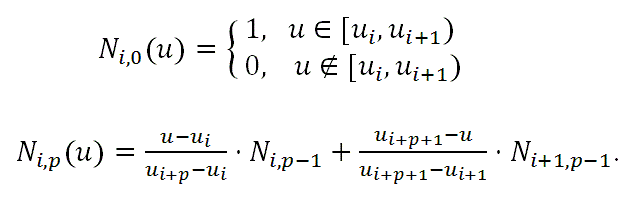
Полуинтервал [u[i], u[i+1])  называется i-тым узловым диапазоном; он может быть нулевой длины, т.к. значения узлов могут быть одинаковы.

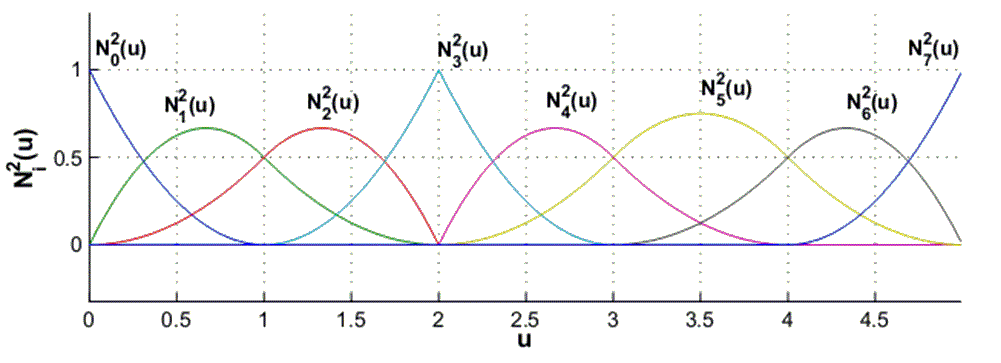
Рисунок 1. Квадратичные базисные функции определенные на узловом векторе U = {0,0,0,1,2,2,3,4,5,5,5}

Узловой вектор представляет собой последовательность значений параметров, которые определяют, где начинается и заканчивается базисная функция. Существует два типа узловых векторов: однородные и неоднородные. В однородных узловых векторах значение узлов распределены в векторе с одинаковым шагом, и поэтому в нем нет повторяющихся узлов. В неоднородном векторе значение узлом распределены не равномерно, что позволяет контролировать моменты начала и завершения базисной функции. Неоднородные узловые вектора более универсальны, поэтому говоря об узловых векторах мы будем иметь в виду именно неоднородные.

Узел, который повторяется в узловом векторе  раз называют узлом кратности. Свойства базисной функции Б-сплайна: 

–N[i,0](u) ступенчатая функция, равна нулю, если u не принадлежит полуинтервалу [u[i], u[i+1]) и единице в противном случае;

- N[i,p](u) >= 0 при любых i,p и u;

- на узловом интервале [u[i], u[i+1] ), "p+1"-ая базисная функция N[i,p](u) не обращается в ноль, а именно функции N[i-p,p](u),...N[i,p](u).

- если в функции N[i,p](u), в дроби знаменатель обращается в ноль, то вся дробь обращается в ноль;

- Сумма(от j = i-p до i) {N[j,p](u)} = 1 для всех u принадлежащих [u[i], u[i+1] );

- к-ая производная N[i,p](u) будет обозночаться как N[i,p](u) с верхним индексовм (к) в круглых скобках:

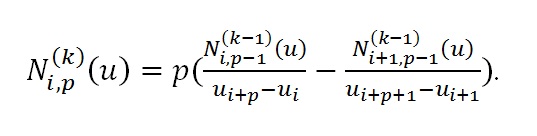
Процесс вычисления базисной функции можно представить в виде следующей схемы:

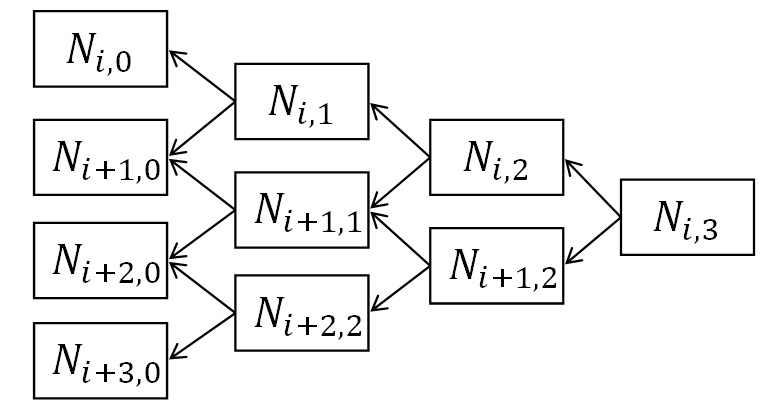
Рисунок 2. Процесс вычисления базисной функции. 

Неоднородные Б-сплайн кривые

NURBS поверхности в однородных координатах степени  в направлении  и степени  в направлении  задается:

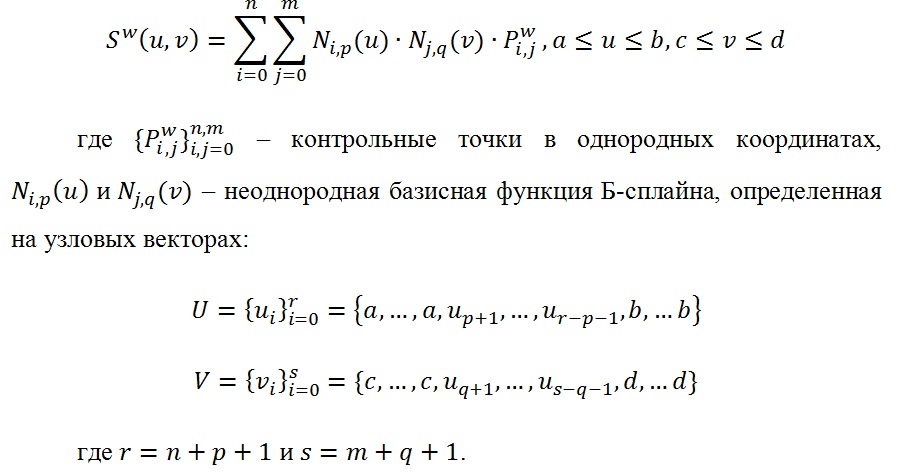
NURBS поверхности имеют следующие важные геометрические свойства, которые в основном аналогичны соответствующим свойствам NURBS кривых:

- граничные значения: S(a,c) = P[0,0], S(b,c) = P[n,0], S(a,d) = P[0,m];

- аффинные преобразования применимы к NURBS поверхностям, т.к. аффинные преобразования применяются к ее контрольным точкам;

- если (u,v) принадлежит [ui, ui+1 ) x [vi, vi+1), то S(u,v) определяется выпуклой оболочкой из контрольных точек Pi-p,j-q,..Pi,j;

- локальная модификация: изменение Pi,j или wi,j изменяет поверхность S(u,v) только на прямоугольнике [ui, ui+p+1) x [vj, vj+q+1);

- дифференцируемость: S(u,v) является p-k раз дифференцируемой по u на узле кратности k, и раз q-k дифференцируемой по v на узле кратности k.

Алгоритмы поиска точек пересечений луча и NURBS поверхности.

Первый алгоритм появился еще в 1980 году, и с тех пор появилось достаточно много подходов к решению этой проблемы [12] [5]. Но можно выделить лишь несколько основных алгоритмов, поскольку все остальные являются лишь их модификацией. Можно выделить два основных алгоритма, которые не использую тесселяцию:

- итерационный метод Ньютона (Toth, 1985)

- метод отсечения Безье (Nishita, 1990) [9]

Оба метода позволяют численно находить точку пересечения луча и NURBS поверхности. Перед тем как мы перейдем к рассмотрению этих методов необходимо ввести некоторые обозначения.

Метод ньютона

Пусть у нас есть NURBS поверхность, заданная в виде:

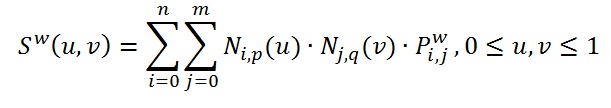
Луч R(t), заданный в параметрическом виде: R(t) = o + d*t, где  o – позиция, d – направление. Представим луч также как пересечение двух ортогональных плоскостей и  (Рисунок 3).

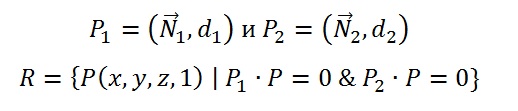
Где N1 и N2 – нормали плоскостей, d1 и d2 – расстояние от плоскости до начала координат.

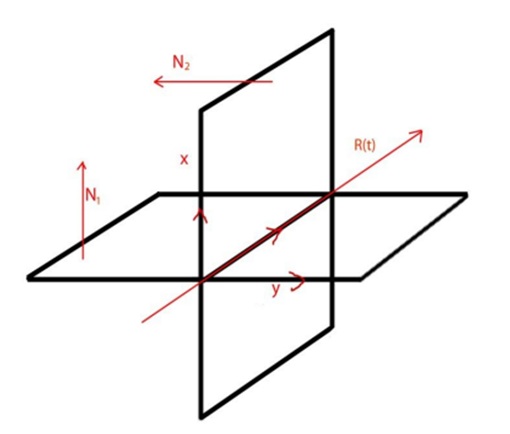
Рисунок 3. Луч, как пересечение плоскостей

Определим функции d1(u,v) и d2(u,v), возвращающие расстояние от точки поверхности до плоскостей P1 и P2:

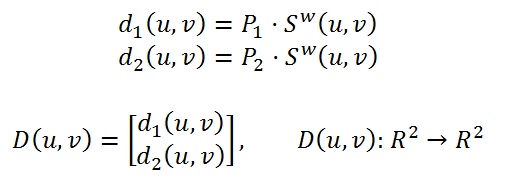
Где матрица Якоби и обратная матрица Якоби вычисляются следующим образом:

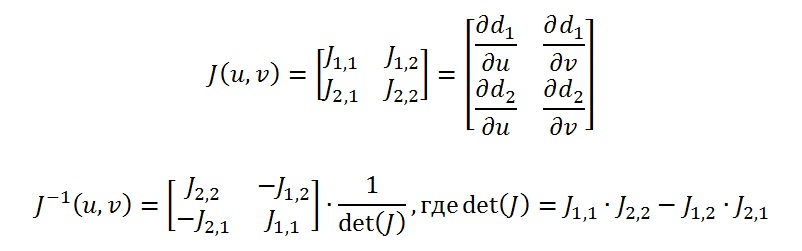
где rand(0,1) – случайное вещественное число  на полуинтервале [0,1).

Итерационный процесс продолжается до тех пор, пока не выполнится одно из следующих условий:

1. || D(ui,vi) || > || D(ui-1,vi-1) || если новая оценка увеличивает расстояние до луча, то будем считать что, луч не пересекает поверхность;

2. ui,vi не принадлежат отрезку [0,1], случай рассматривается ниже;

3. i > max, в случае превышения количества итераций считаем, что пересечения нет;

4. || D(ui,vi) || < epsilon, считаем значения (ui,vi) решением.

В случае, когда ui,vi не принадлежат отрезку [0,1], мы могли бы просто считать что, луч не пересекает поверхность, но это приводит к погрешностям на краях поверхности. Это проблема может быть решена следующим образом. Если ui,vi не принадлежат отрезку [0,1], то мы их зеркально отображаем, чтобы поместить их в область параметров: (ui = -ui если ui < 0) и (ui = 2-ui если ui > 1). Аналогично с параметром vi. Если || D(ui,vi) || < epsilon, то считаем (ui,vi) решение, в противном случае пересечения нет. Норма D(ui,vi) - евклидово расстояник в даумерном пространстве (u,v).

Метод отсечений безье

Пересечение плоскости Pk, k= [1,2]  и поверхности можно записать как:

В этой проекции плоскость P1 становится осью y, плоскость P2 осью x, а луч проецируется в начало координат.

Сначала мы определим два вектора Lu и Lv  и  в системе координат:

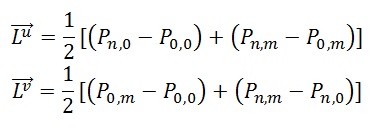
Вектор Lu  должен быть перпендикулярен направлению u, а вектор Lv  перпендикулярен направлению v. В этом случае алгоритм отсечения Безье сходится к правильному решению более быстро. Если угловые точки поверхности совпадают, то мы получим нулевые векторы. Этого можно избежать следующим образом:

- если нулевой только один вектор, то его мы берем перпендикулярным не нулевому вектору;

- если оба вектора нулевые, то вычисляем вектора среди других контрольных точек.

Чтобы найти решение уравнения P(u,v) = 0  для направлений Lu и Lv, необходимо выполнить следующий итерационный процесс:

1. Разобьём параметрическую область uv = [a,b] x [c,d] на сетку размером n*m. Шаг по u равен (b-a)/n, по v равен (d-c)/m. Каждому узлу сетки соответствует точка Ci,j = P(ui,vi), i принадлежит интервалу [0,n], j - интервалу [0,m];

2. Определим двумерное пространство (u,d), состоящего из точек вида: Di,j = (ui,di,j), где di,j  знаковое расстояние от точки Ci,j до прямой проходящей через начало координат и направляющим вектором Lu. Аналогично для направления v.

3. В пространстве (u,d) находим отрезок [umin, umax], на котором d(u) = 0. Аналогично находим [vmin, vmax].

Повторяем процесс для области [umin, umax] x [vmin, vmax].

Итерационный процесс завершается в двух случаях:

1. Если на третьем шаге нет значений, на которых d(u)=0 , считаем, что луч не пересекает поверхность.

2. Если размер области меньше некоторого малого значения, считаем, что луч пересекает поверхность в точке с параметрами u = 0.5*(umin + umax), v = 0.5*(vmin + vmax).

NURBS поверхность строиться одинаково, как при использовании итерационного метода Ньютона, так и при использовании метода отсечения Безье.

Итерационный метод Ньютона хоть и является наиболее простым и понятным, но у него есть один существенный недостаток, который выявился в результате тестирования программы. Он существенно зависит от начального приближения. Т.е. если в качестве первого приближения взять, какие то конкретные , то метод может долго сходится к решению или вовсе его не найти. Поэтому, что бы найти наилучшее приближение мы разбиваем нашу плоскость по параметрам на сетку с определенным шагом. В каждом узле сетки считаем точку, которая соответствует этим параметрам. В результате, в качестве первого приближения мы берем ту пару , которой соответствует точка, находящаяся ближе всего к лучу. Данный метод позволяет найти достаточно хорошее приближение и поэтому итоговое решение находится примерно за 5 шагов итерационного метода.

Метод отсечения Безье не требует каких-либо начальных значений, а значит, он более подходит для решения данной проблемы. Единственная сложность, которая возникла в процессе реализации, это определение максимального и минимального значения параметров, на третьем шаге итерационного процесса. Необходимо следить за тем, чтобы интервал не оказался равным нулю или наоборот занимал всю область значений. В этих случаях итерационный процесс может выдать ложное решение или не сходится к решению.

Рисунок 4. Результат работы трассировщика лучей с NURBS поверхностью.

Для решения этой задачи наиболее подходит метод отсечения Безье. Он не зависит от начальных условий и в большинстве случаев позволяет получить NURBS поверхность без артефактов. Существует несколько проблем, но по сравнению с основной проблемой итерационного метода Ньютона, они менее значительные. Говоря в общем, о применении NURBS поверхностей в трассировке лучей, трассировка NURBS значительно увеличивает время рендеринга сцены по сравнению с трассировкой других видов поверхностей.

Литература

• 1. Piegl, L., Tiller, W. The NURBS Book. Second edition. New York: Springer, 1996. 646 P.
• 2. Wald, I. Realtime Ray Tracing and Interactive Global Illumination. Germany: Saarland University, 2004. 297 P.
• 3. Shirley, P., Morley, K. Realistic Ray Tracing. Second edition. Massachusetts: A K Peters, 2003. 239 P.
• 4. Efremov, A., Havran, V., Seidel, H. Robust and Numerically Stable Bezier Clipping Method for Ray Tracing NURBS Surfaces. Germany: Computer Science Department University of Saarland, 2005.
• 5. Efremov, A. Efficient Ray Tracing of Trimmed NURBS Surface. Germany: Computer Science Department University of Saarland, 2004.
• 6. Martin, W., Cohen, E., Fish, R., Shirley, P. Practical Ray Tracing of Trimmed NURBS Surfaces. University of Utah.
• 7. Kajiya, J. Ray tracing parametric patches. Computer Graphics (SIGGRAPH ’82 Proceedings), 1982, 16(3).
• 8. Barth, W., Sturzlinger, W. Efficient ray tracing for Bezier and B-spline surfaces. Computers and Graphics, 1993, 17(4).
• 9. Nishita, T., Sederberg, W. Ray Tracing Trimmed Rational Surface Patches. Computer Graphics, 1990, 24(4).
• 10. Glasner, A., An introduction to Ray Tracing. 1989.
• 11. Rogers, D. An Introduction to NURBS: with historical perspective. 1^st edition, 2000.
• 12. Espinio, F., Boo, M., Amor, M. Adaptive Tesselation of NURBS Surfaces. Journal of WSCG, 2003.
• 13. Non-uniform rational B-spline. URL: http://en.wikipedia.org/wiki/Non-uniform_rational_B-spline.