|
Bounding Volume Hierarchy (BVH) - Иерархия ограничивающих объемов. Исторически BVH деревья используются для рассчета столкновений (физика). Однако в последнее время BVH активно стараются задействовать в рейтрейсинге в связи с тем, что в анимированных сценах BVH можно быстрее перестраивать, и как правило можно перестраивать не все дерево.
Очевидно, что разновидностей BVH деревьев можно придумать сколько угодно. Достаточно взять некую произвольную фигуру и использовать ее в качестве ограничивающего объема. Исторически выделяют 5 типов BVH деревьев:
-
Sphere tree
-
AABB tree (Axis Aligned Bounding Box)
-
OBB tree (Oriented Bounding Box)
-
k-DOP (Discrete Oriented Polytope)
-
SSV (Swept Sphere Volume)
Чем сложнее ограничивающий объем, тем лучше адаптивность, но тем сложнее дерево строить и траверсить. Далее по тексту будет считаться, что речь идет только о бинарных BVH деревьях. Читателю предлагается обобщить алгоритмы на случай n-арного дерева самостоятельно.
Object and Spatial split
Когда речь заходит о BVH, существует небольшая, но довольно существенная путанница в том, какие примитивы включать в дочерние узлы при построении и как именно производить разбиение. Вопрос, который порождает путанницу звучит так:
"Что делать, если примитив пересекает оба дочерних узла?". Существует 2 стратегии, которые в принципе можно смешивать.
При разбиении типа "Object split" необходимо просто найти разбиение нашего исходного множества примитивов на 2 подмножества. Затем посчитать ограничивающий обьем для обоих подмножеств и дело сделано. В этом случае ответ на поставленные ранее вопрос звучит так:
"Такой примитив всегда идет в тот узел, в котором он содержится полностью." Такой узел всегда существует (просто по построению самого "Object Split" разбиения).
При разбиении, называемом "Spatial Split" как правило выбирается некая плоскость, по который мы стараемся поделить пространство на 2 части (эта плоскость, вообще говоря, может быть и не параллельна осям координат). В этом случае нам необходимо проверять каждый примитив на пересечение с ограничивающими боксами обоих дочерних узлов. И ответ на поставленный выше вопрос для "Spatial Split" звучит так:
"Такой примитив нужно добавлять в каждый из дочерних узлов, который он пересекает."
Однако здесь следует сделать одну оговорку. Если дерево строится смешанной стратегией, то поиск в нем все-равно нужно будет выполнять так, как если бы оно полностью строилось при помощи стратегии "Object Split", поскольку в таком дереве возможны пересечения дочерних узлов. И в этом случае можно немного ослабить критерий:
"Такой примитив идет в тот узел, в котором он содержится полностью, либо если такого узла нет, примитив нужно добавлять в каждый из дочерних узлов, который он пересекает."
Такой критерий может помочь, если плоскость, которой пространство делится на 2 части не параллельна осям координат или используется нетипичный вид BVH дерева (не AABB).
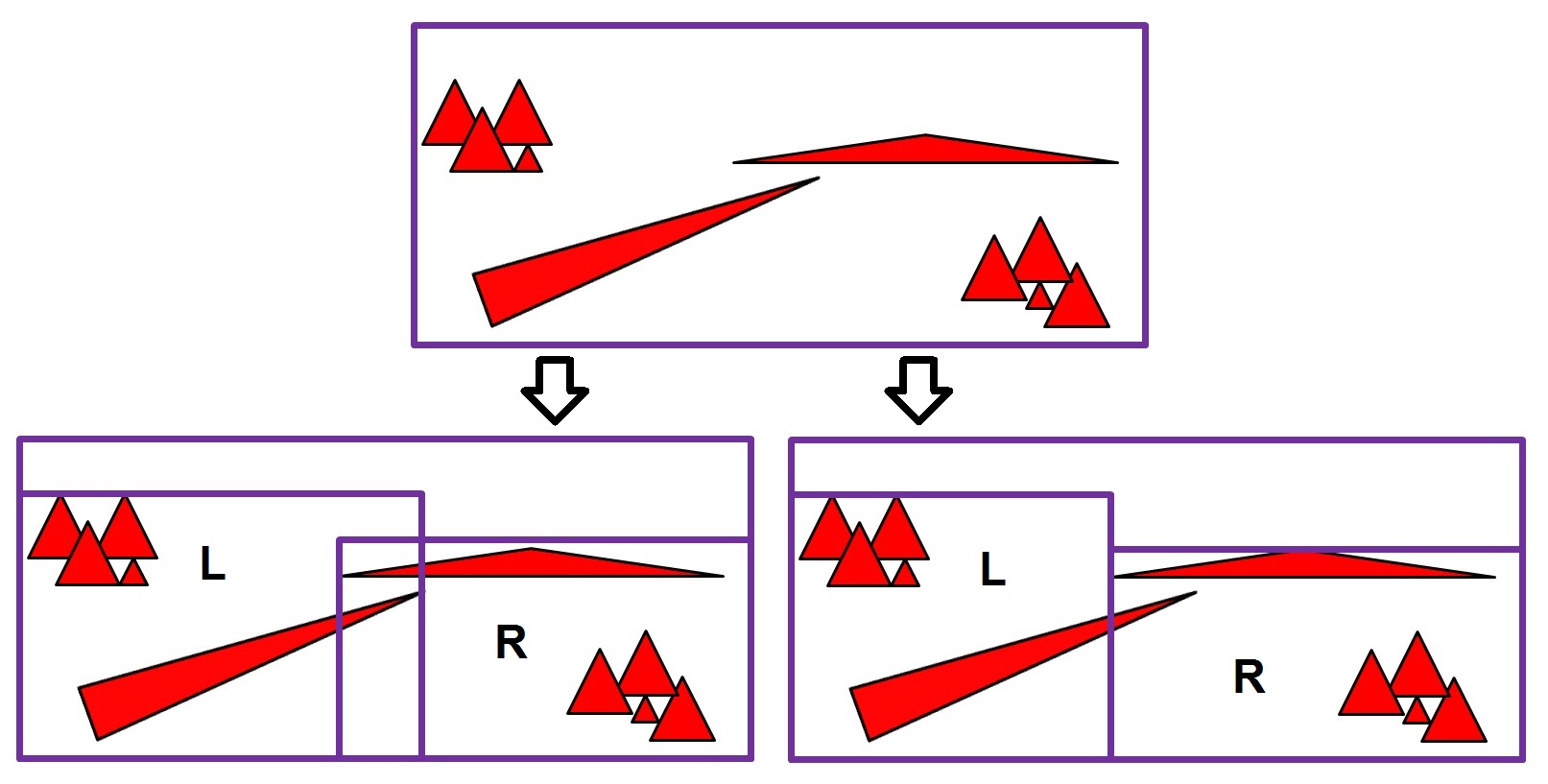
Рисунок 0. Object Split (справа) и Spatial Split (слева).
Тонкий длинный треугольник справа при стратегии разбиения "Object Split" попадет только в левый узел ("L"). А при стратегии разбиения "Spatial Split" он попадет в оба дочерних узла ("L" и "R"). Spatial Split больше похоже на kd-дерево. При поиске в таком дереве можно остановиться, если первое найденное пересечение лежит внутри листа, в котором мы ищем (можно найти пересечение с примитивом и вне листа). Если же применяется стратигия Object Split, то останавливать поиск в таком дереве на первом пересечении нельзя. Нужно искать до тех пор, пока стек не пуст. Мы вернемся к этому позже.
Касательно смешанной стратегии построения BVH - она имеет смысл. Однако вместо нее удобно использовать технику, называемую "Early Split Clipping". Далее по тексту эта техника будет рассмотрена.
Sphere tree
Sphere tree плохо тем, что оно весьма неадаптивно, то есть медленно приближает геометрию. Каждый узел обладает большим количеством пустого пространства. Но зато со сферами очень просто считать пересечения, в том числе лучами. И сферическое дерево относительно просто строить. Вот здесь можно найти целую пачку алгоритмов построения дерева из сфер а также готовый тулкит. Другое дело, что в рейтрейсинге, в конечном итоге придется перебрать довольно много сфер (из-за плохой адаптивности). Sphere tree хорошо подходит для разреженной и относительно равномерной геометрии. Однако, несмотря на недостатки BVH дерева из сфер, уже довольно давно существует интерактивный трассировщик лучей, использующий его - Virtual Ray (рис. 1).
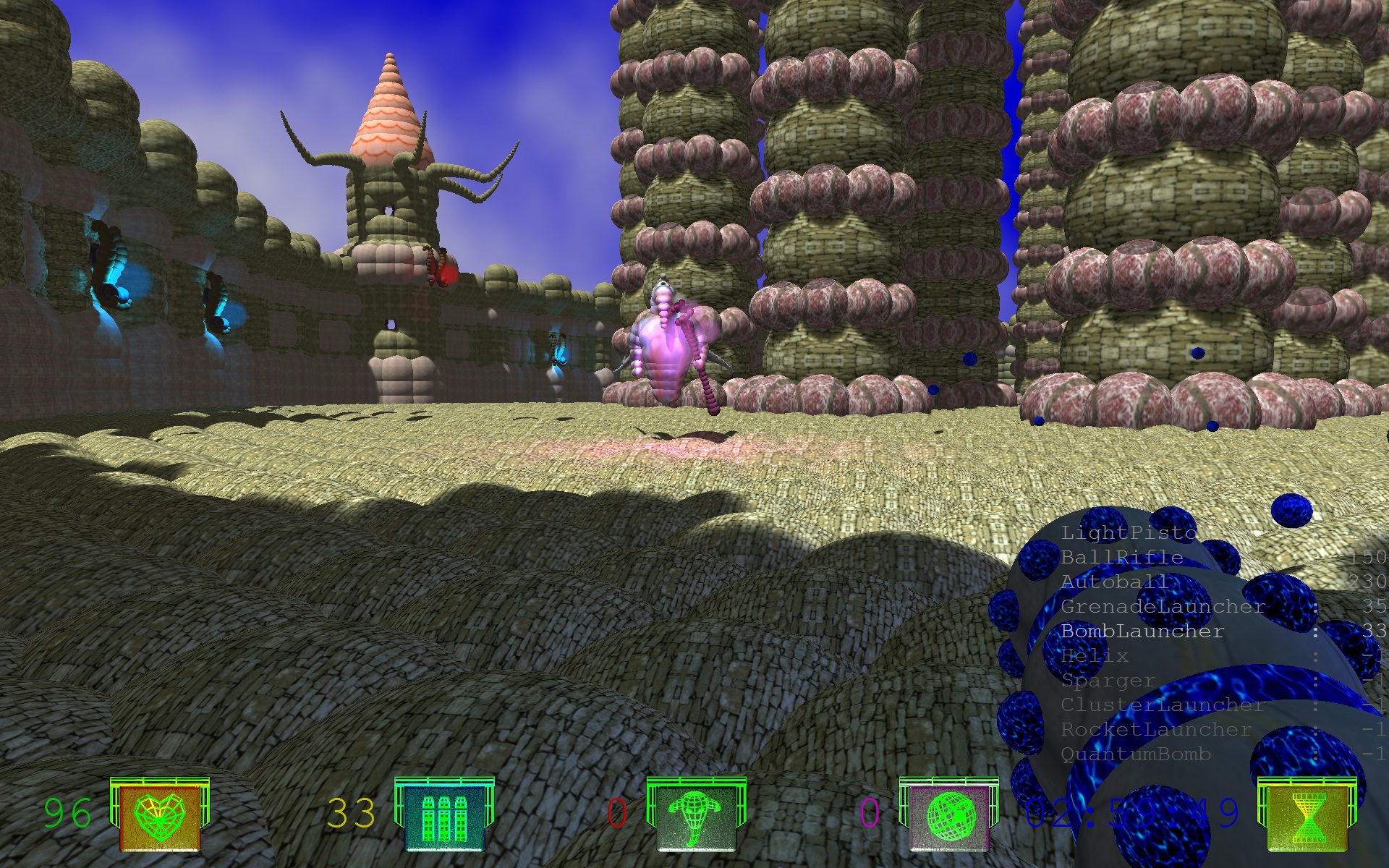
Рисунок 1. Virtual Ray.
AABB tree
Чаще всего используется именно этот вид дерева. AABB намного лучше подходят в качестве ограничивающего объема чем сферы. Также хорошо, что с AABB довольно легко считать пересечения. Существутет оптимизированный вариант на SSE или без него (просто на С++). В библиотеке MGML вы можете найти оба.
Построение AABB дерева
Рассмотрим алгоритм построение AABB дерева. Практически все, что будет изложено для AABB можно с небольшими модификациями применить и для остальных видов BVH деревьев.
Алгоритм построения оптимального AABB столь-же сложен, сколь и алгоритм построения хорошего kd-дерева (даже чуть сложнее). Когда мы строим kd-дерево, то на каждом шаге подразбиения минимизируем функцию стоимости SAH. В случае kd-дерева все довольно просто, потому что мы вибираем только плоскость разбиения и можем просто перебрать все возможные границы примитивов по трем измерениям (обычно SAH вычисляют на границах), чтобы найти такую плоскость, в которой функция SAH будет минимальна. То есть нам нужно вычислить SAH лишь 6*N раз (где N- количество примитивов) и найти минимум.
В случае BVH, все сложнее, потому что вариантов возможных разбиений не 6*N а 2 в степени N. Перебрать их все не представляется возможным. Все дело в том, что в отличие от kd дерева, BVH на каждом уровне вообще говоря может произвести разбиение на 2 совершенно произвольных подмножества примитивов. Всего таких подмножеств 2 в степени N.
Быстрое и качественное построение AABB
Однако можно использовать упрощение, не сильно ухудшающее качество дерева, но позволяющее значительно упростить процедуру построения дерева. Фактически, с помощью этой процедуры можно свести построение дерева к сортировке!. Поэтому на практике BVH строить во много раз проще, чем kd-tree!
Предлагается следующий алгоритм. Строим дерево сверху вниз. На каждом уровне BVH дерева сортируем все примитивы по максимому ограничивающих боксов по осям X, Y и Z (на самом деле можно выбрать и другой признак). Таким образом у нас получается 3 массива. Первый отсортирован по X-ам, второй по Y-кам и третий по Z. Затем мы для каждого массива просто перебераем вcе разбиения на подмножества следующего вида:
[0, 1..n]
[0..1, 2..n]
[0..3, 4..n]
...
[0..n-1, n]
Для каждого из этих разбиений считаем SAH. Запоминая каждый раз ограничивающие AABB в специальном массиве для получаемых подмножеств (rightBounds) мы можем не пересчитывать эти AABB полностью, что сводит наш поиск всего к 2 проходам по массиву. С конца к началу и с начала к концу.
Так как каждый массив мы заранее отсортировали по соответсвущей оси, то скорее всего выбранные таким образом разиения позволят минимизировать самопересечения и дадут более-менее хороший SAH.
Ниже приведен фрагмент исходного кода построителя:
////////////////////////////////////////////////////////////////////////////
////
SplitData FindObjectSplit(PrimitiveList& a_plistX, PrimitiveList& a_plistY, PrimitiveList& a_plistZ, const AABB3f& a_box)
{
struct BoxLessMax
{
BoxLessMax(int a) { axis=a; }
bool operator()(const PrimitiveRef& p1, const PrimitiveRef& p2) const
{ return (p1.Box().vmax[axis] < p2.Box().vmax[axis]); }
int axis;
};
PrimitiveList* plists[3] = {&a_plistX, &a_plistY, &a_plistZ};
BVHTree::SplitData res;
res.sah = SAH_OVERSPLIT_TRESHOLD*SurfaceArea(a_box)*a_plistX.size(); // SAH_OVERSPLIT_TRESHOLD usually equals to 1.0f
res.subdivideNext = false;
res.axis = -1;
std::vector<AABB3f> rightBounds(a_plistX.size());
for (int dim=0;dim<3;dim++)
{
// sort data according to axis
//
PrimitiveList& plist = *plists[dim];
std::sort(plist.begin(), plist.end(), BoxLessMax(dim));
// Sweep right to left and determine bounds.
//
AABB3f rightBounds1;
for (uint i = plist.size() - 1; i > 0; i--)
{
rightBounds1.include(plist[i].Box());
rightBounds[i-1] = rightBounds1;
}
// Sweep left to right and select lowest SAH.
//
AABB3f leftBounds;
for (uint i = 1; i < plist.size(); i++)
{
leftBounds.include(plist[i-1].Box());
float sah = EMPTY_NODE_COST_TRAVERSE + SurfaceArea(leftBounds)*(i) + SurfaceArea(rightBounds[i-1]) * (plist.size() - i);
if (sah < res.sah)
{
res.sah = sah;
res.axis = dim;
res.primsOnLeftSide = i;
res.primsOnRightSide = plist.size() - i;
res.leftBounds = leftBounds;
res.rightBounds = rightBounds[i-1];
}
}
} // for (int dim=0;dim<3;dim++)
res.subdivideNext = (res.axis != -1) && (res.sah < SAH_OVERSPLIT_TRESHOLD*SurfaceArea(a_box)*a_plistX.size());
return res;
}
Разумеется, этот вариант построения не единственный. Весь вопрос в том, как быстро выбирать разбиения множества примитивов на такие два подмножества, чтобы получался минимальный SAH.
Early Split Clipping
У AABB дерева есть один существенный недостаток: треугольники на самом деле плохо приближаются боксами. Даже Axis Aligned (те которые лежат в плоскости x,y или z) треугольники обладают площадью поверхности, вдвое меньшей чем ограничивающих их бокс. Посмотрите на рисунок 1.а.
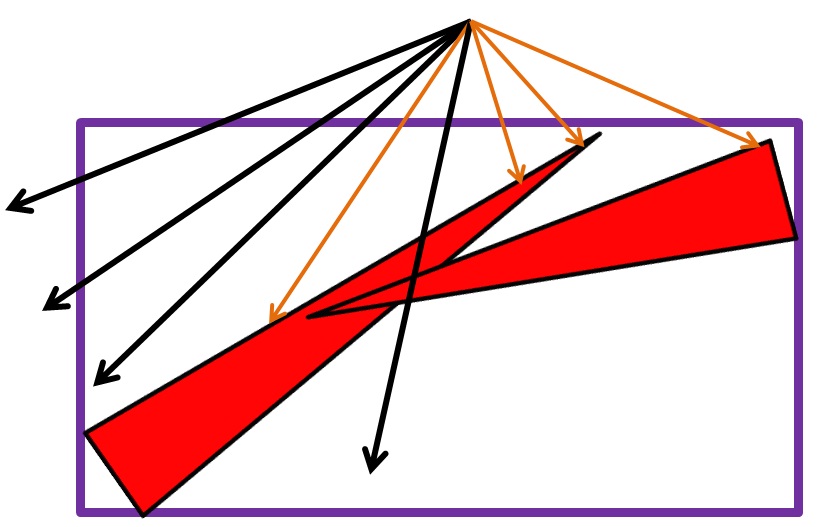
Рисунок 1. а.Обычный лист BVH без использования техники Early Split Clipping.
Проблемма здесь в том, что через ограничивающий бокс треугольника проходит значительное количество лучей, которые на самом деле не пересекают этот треугольник (треугольник плохо приближается боксом). На рисунке 1.б. черным цветом обозначены лучи которые не пересекли ни один треугольник (представьте эту картинку в 3D). Если в геометрии примутствует много длинных и тонких треугольников, получается BVH с огромным количеством самопересекающихся узлов, содержащих много пустого пространства. Чтобы побороть этот недостаток, можно отесселировать треугольник, подразбив его на более мелкие, но существует более элегеантное и экономное в плане памяти решение, называемое "Early Split Clipping".
Предлагается представлять треугольник не одним боксом а несколькими. То есть один длинный треугольник скармливается BVH построителю в виде набора боксов, содержащих ссылки на этот треугольник.
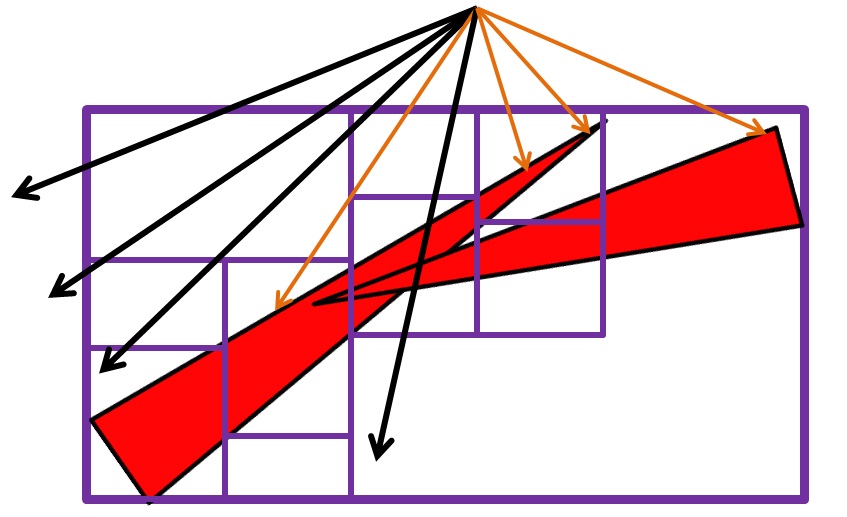
Рисунок 1. б. Заранее подразбитый треугольник (левый), эта картинка НЕ отражает лист BVH дерева.
А затем BVH строится как обычно, искользуюя только технику "Object Split". Важно отметить, что рисунок 1. б. не отражает узел BVH дерева, а обозначает только заранее подразбитый треугольник. Как будет выглядеть BVH дерево и где тут получаться листья еще предстоит решить построителю дерева.
Если просто взять лист BVH дерева (рис. 1.а), и разбить его в стиле рисунка 1.б., то получится техника называемая "Late Split Clipping". Известно, что она не дает ускорения [1].
Поиск в BVH
Алгоритм траверса со стеком
Идея заключается в следующем: рекурсивно обходим дерево, каждый раз выбирая ближайший узел при спуске. На каждом шаге считаем пересечение луча с обоими боксами, выбираем ближайший бокс и переходим в него. А дальний помещаем в стек (если конечно луч пересекает оба узла). Если луч пересекает только один узел просто переходив в него. Если луч не пересекает ни одного узла, достаем узлы из стэка. К сожалению, нельзя остановить траверс BVH если мы нашли первое пересечение, лежащие внутри какого-либо листа (в kd-tree мы могли в таком случае остановить поиск). Так как в BVH возможны самопересекающиеся узлы, мы обязаны продолжить траверс до тех пор, пока стэк не пуст. Однако, если мы видим, что ограничивающий бокс узла лежит дальше, чем уже найденное пересечение, мы можем не траверсить этот узел.
#define STACK_SIZE 64
struct TraversalStackElement
{
float t_far;
int offset;
};
////////////////////////////////////////////////////////////////////////////
////
void BVHTraversal(float3 ray_pos, float3 ray_dir, Lite_Hit* pClosestHit)
{
TraversalStackElement stack[STACK_SIZE];
int top=0;
stack[0].t_far = INFINITY; // this is need
*pClosestHit = Lite_Hit::NONE; // no intersection found
int leftNodeOffset = 1;
float3 invDir = SafeInverse(ray_dir);
while (true)
{
// traversal code
//
while (true)
{
BVHNode leftNode = GetBVHNode(leftNodeOffset);
BVHNode rightNode = GetBVHNode(leftNodeOffset+1); // right node
int leftRightOffsetAndLeaf = rightNode.m_leftOffsetAndLeaf;
int leftLeftOffsetAndLeaf = leftNode.m_leftOffsetAndLeaf;
float c0min = 0;
float c1min = 0;
bool traverseChild0 = RayBoxIntersection(ray_pos, invDir, leftNode.box, &c0min);
bool traverseChild1 = RayBoxIntersection(ray_pos, invDir, rightNode.box, c1min);
traverseChild0 = traverseChild0 && (pClosestHit->t >= c0min);
traverseChild1 = traverseChild1 && (pClosestHit->t >= c1min);
// traversal decision
//
if (traverseChild0 && traverseChild1)
{
// determine nearest node
//
stack[top].t_far = fmaxf(c1min,c0min);
stack[top].offset = (c0min <= c1min) ? leftRightOffsetAndLeaf : leftLeftOffsetAndLeaf;
leftNodeOffset = (c0min <= c1min) ? leftLeftOffsetAndLeaf : leftRightOffsetAndLeaf;
top++;
}
else if (traverseChild0 && !traverseChild1)
leftNodeOffset = leftLeftOffsetAndLeaf;
else if (!traverseChild0 && traverseChild1)
leftNodeOffset = leftRightOffsetAndLeaf;
else // both miss, stack.pop()
{
if (top==0)
return;
do
{
top--;
leftNodeOffset = stack[top].offset;
}
while (top != 0 && pClosestHit->t < stack[top].t_far);
}
if (BVHNode::IS_LEAF(leftNodeOffset))
break;
leftNodeOffset = BVHNode::EXTRACT_OFFSET(leftNodeOffset);
} // end traversal code
// intersection code
//
do
{
int primsListOffset = BVHNode::EXTRACT_PRIMITIVE_LIST_OFFSET(leftNodeOffset);
IntersectAllPrimitivesInLeaf(ray_pos, ray_dir, primsListOffset, pClosestHit);
if (top==0)
return;
do
{
top--;
leftNodeOffset = stack[top].offset;
} while (top != 0 && pClosestHit->t < stack[top].t_far);
} while (BVHNode::IS_LEAF(leftNodeOffset));
leftNodeOffset = BVHNode::EXTRACT_OFFSET(leftNodeOffset);
}
}
Заметим, что во время спуска по дереву мы каждый раз идем в ближайший узел. Это очень важно для трассировки лучей, так как позволяет достаточно рано найти пересечение и не искать его во всех узлах, которые лежать дальше него.
Алгоритм траверса без стека (для GPU)
Существует алгоритм поиска в BVH дереве и без стека. К сожалению, он менее эффективен. Его отличительной чертой является то, что луч придется пересекать со всеми примитивами вдоль его пути. Нельзя остановить поиск, найдя только первое пересечение.
Для того чтобы обходить BVH дерево без стека нужно добавить так называемы "escape index" - некая ссылка на следующий узел дерева, который нужно траверсить:
-
В каждом левом подузле запомнить ссылку на правый.
-
В каждом правом запомнить ссылку на тот узел, на который ссылается его родитель.
-
Обход будем осуществлять в порядке строго слева направо.
На рис. 2 показан пример того "escape index" синими стрелками. Следует отметить, что номерация узлов может напрямую соответствовать их адресам в памяти. То есть элемент с номером (0) первым в массиве узлов, (1) вторым и.т.д.
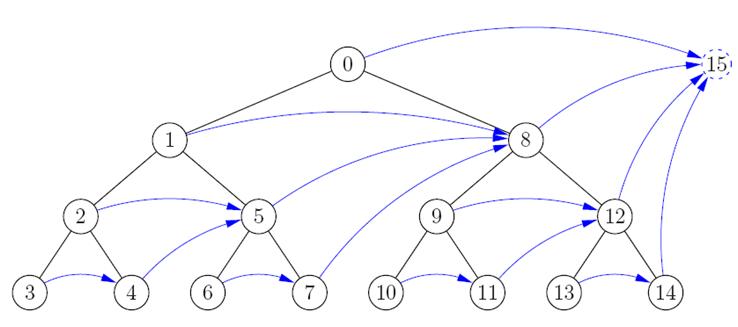
Рисунок 2. Escape index в BVH дереве.
Начинаем поиск с корня. Проверяем левый узел (1). Предположим что луч его пересекает. Тогда переходим в узел (1) и снова проверяем его левого потомка (2). Предположим, что луч его не пересекает. Тогда по "escape index" переходим в узел (5) и проверяем его. Если луч пересекает узел (5) мы обязаны проверить его левого потомка (6); иначе, перейти в узел (8). То есть основное правило следующее: Если луч пересекает узел, мы обязаны проверить его левого потомка. Иначе выйти по "escape index"-у. Что касается пересечений луча и треугольника, мы должны будем проверить все листья которые пересек луч и найти ближайшее пересечение.
curr_node = root;
while (curr_node.Valid())
{
float min_t = INFINITY;
Hit min_hit = NONE; // пока что нет объекта, с которым бы пересекся луч
if (!curr_node.Leaf())
{
(t, hit) = IntersectAllPrimitivesInLeaf(curr_node);
if (t < min_t)
{
min_t = t;
min_hit = hit;
}
curr_node =curr_node.EscapeNode();
}
else
{
if (IntersectRayBox(ray, curr_node.Box()))
curr_node = curr_node.Left();
else
curr_node = curr_node.EscapeNode();
}
}
Таким образом, алгоритм в случайном порядке (в смысле ближний-дальний) перебирает все листья BVH дерева с которыми пересекся луч. Поэтому необходимо искать минимум на всем пути луча. В результате получается очень простой (проще чем со стеком) но отчасти переборный алгоритм. На самом деле описанная схема крайне эффективна для определения столкновений - если поиск осуществляется непротяженными объектами - такими как сфера, AABB. В этом случае порядок обхода узлов не имеет значения.
OBB tree (Oriented Bounding Box)
Это дерево из обычных (не выровненных по осям координат) паралеллепипидов. Считается, что оно имееит лучшую адаптивность, чем AABB tree. Однако его сложнее строить и траверсить (производить поиск, прослеживать луч).
Построение
Построение OBB будет отличаться от AABB тем, что при разбиении примитивов на 2 подмножества, рассчет OBB для дочерних узлов выглядит немного сложнее.
Итак, пусть у нас дано n точек. Мы хотим определить их ограничивающий OBB. Для этого обычно используется метод главных компонент. Суть проста - нужно посчитать матрицу ковариации, найти ее собственные вектора - они и будут направляющими ограничивающего бокса. Зная направляющие веткора, нетрудно посчитать и размеры бокса. На рис. 3 показаны формулы для рассчета матрицы ковариации. Заметим, что размерность матрицы - 3x3. xi - исходные точки. "мю" - геометрический центр, который считается просто как среднее арифметическое (покоординатно).
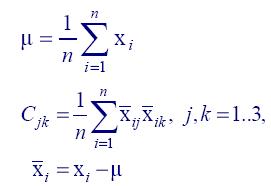
Рисунок 3. Формулы для рассчета матрицы ковариации.
Индекс k здесь - это просто индекс измерения - 0 - x, 1 - y, 2 - z. Поэтому на рис. 3 формула для "xi с чертой" приведена в векторном виде - без уточнения индекса k (то есть, ее нужно повторить для всех k=0..2).
Если на входе массив треугольников, то берут все вершины как точки и по ним строят ограничивающий OBB.
Вопрос о том, как считать пересечения луча и OBB остается открытым (по крайней мере для меня). Самый простой способ - хранить для каждого OBB обратную матрицу преобразования в AABB. Домножать на нее луч и считать пересечение луча и AABB (как в unit-test для пересечения луча и треугольника).
В физике, для определения столкновений OBB используется теорема о разделяющихся осях. Она гласит, что если существует такая ось, что проекции двух фигур на нее не пересекаются, то и объемные фигуры не пересекаются. Для OBB необходимо проверить 6 осей, параллельных граням и 9, параллельных ребрам. В итоге это выливается в 9 векторных произведений, 15 проекций и 15 проверок типа if (a < b). Сравните, в AABB нужно было всего лишь 3 проверки и никаких вычислений.
k-DOP (Discrete Oriented Polytope)
k-DOP - структуры - это иерархические BVH деревья, состоящие из дискретно-ориентированных многогранников. В качестве ограничивающегно примитива выбирается многогранник, грани которого ориентированны в пространстве строго определенным образом (рис 3).
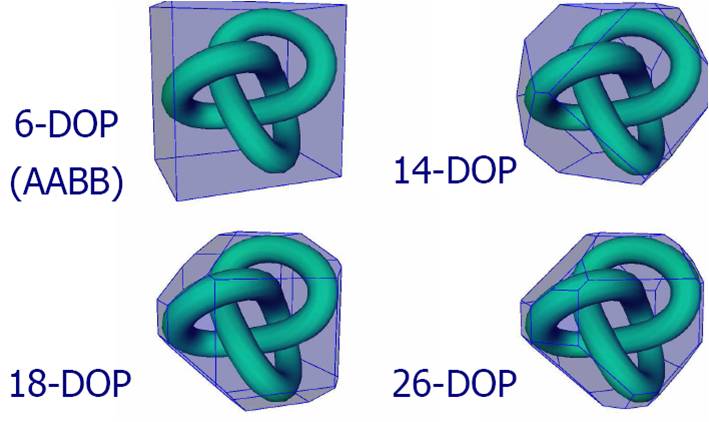
Рисунок 3. Дискретно-ориентированный многогранник (k-DOP).
На самом деле k-DOP структуры не сложнее чем AABB. Разница лишь в том, что ограничивающих плоскостей не 6 а больше. Весь код рейтрейсинга или коллижен-детекшена остается практически идентичным за исключением того, что нужно просто больше плоскостей. Например, как посчитать пересечение луча с 14-DOP (рис. 3) ? Для этого сначала надо ответить на вопрос - как мы считали пересечение с AABB. Очень просто, мы пересекали луч со всеми 6-ю плосокстями и искали минимум по t (то есть самое ближайшее). Здесь абсолютно так-же, только нужно перебрать 14 плоскостей и найти минимум. Точно так же можно определять столкновения двух DOP - то есть достаточно просто рассмотреть больше плоскостей.
Как строить такие структуры? - да точно так же как и все другие BVH. Нужно разбить множество примитивов на два подмножества и каждое подмножестов ограничить DOP-ом. Затем, посчитать суммарную SAH для получившихся узлов. Нужно перебрать несколько таких разбиений и найти разбиение с наилучшим SAH.
Как и в случае с AABB для того, чтобы перебрать наиболее вероятные подмножества и быстро определить их ограничивающие объемы, нужно завести несколько массивов (по каждой оси) и отсортировать их например по максимумам. Для AABB мы заводили 3 таких массива, для 14-DOP дерева этих массивов будет 7, для 18-DOP дерева - 9, и.т.д.
SSV (Swept Sphere Volume)

Рисунок 4. SSV ограничивающие примитивы.
Собираем все вместе
Итак, какое же из них лучше? И для чего? Обычно все используют AABB из-за его простоты. Также немаловажным фактором является то, что реальная геометрия достаточно хорошо приближается AABB. Скажем, если у нас имеется город, где дома прямоугольные, то нет смысла изобретать какие-то более сложные структуры чем AABB дерево. Хотя существуют работы где люди считают адаптивность деревьев. ЧТобы понять, как оценивается адаптивность, мы рассмотрим такое понятие как сходимость в метрике Хаусдорфа. Если кто испугался, то не зря, потому что нам придется залезть в Функциональный Анализ.
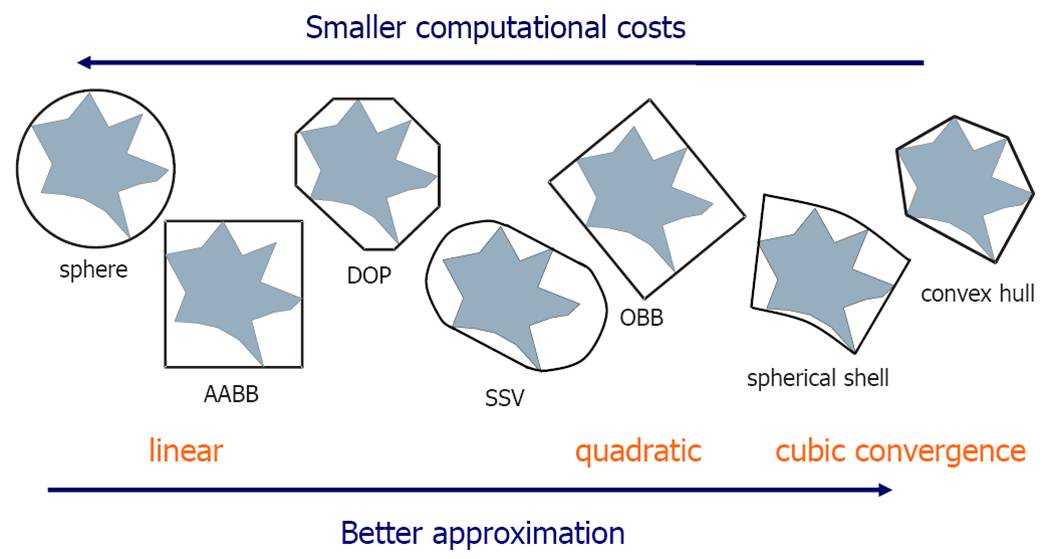
Рисунок 5. Сходимость множества точек дерева к множеству точек геометрии в метрике Хаусдорфа. В качестве геометрии рассматривался тор.
Формально, метрика Хаусдорфа определяется так: 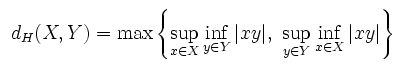
где X и Y - два компактных подмножества некоторого метрического пространства. В применениии в BVH деревьям, метрика Хаусдорфа может быть рассчитана следующим образом:
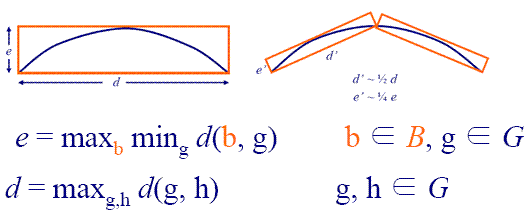
Рисунок 6. Рассчет метрики Хаусдорфа для BVH дерева и геометрии типа "тор".
Все понятно? - отлично. Нет? - не расстраивайтесь, особого смысла в этих оценках нет. Как уже было сказано, считать какую-то сходимость в отрыве от реальной геометрии бессмыслененно! Далеко не вся геометрия похожа на тор (картинка приведена именно для тора), поэтому рисунок 5 не стоит воспринимать как непреложную истину.
Заключение
В целом, BVH - очень хорошее решение. Они обладают высокой адаптивность, хорошей скоростью построения, тратят заранее известное количество памяти (object split). И в конце концов, их довольно просто травесить как для трассировки лучей, так и для определения столкновений. На CPU и на GPU. BVH - это вещь, используйте BVH.
Литература
[1] Early Split Clipping for Bounding Volume Hierarchies. Manfred Ernst∗ G¨unther Greiner†, Lehrstuhl f ¨ur Graphische Datenverarbeitung, Universit ¨at Erlangen-N¨urnberg, Germany
|