Алгоритм Distance-aided Ray Marching

В случае сложных поверхностей, не нужно искать пересечение так, как это делают обычно – вычисляя геометрически пересечения прямой и поверхности явно. Вместо этого существует простой алгоритм, позволяющий сделать это итеративно, даже для тех поверхностей, для которых явная формула пересечения луча и поверхности вообще не существует (или ее очень сложно вывести).

Пусть существует функция f(x,y,z), задающая поверхность уравнением вида f(x,y,z) = 0. Для краткости можно будем писать f(p) = 0.

Функции есть тут: http://www.iquilezles.org/www/articles/distfunctions/distfunctions.htm

Если в функцию f вместо p подставить, некоторую точку, не лежащую на поверхности, мы получим некое не равное нулю число. Нетрудно заметить, что это число будет представлять собой знаковое (хотя это может зависеть от формулы) расстояние до поверхности.

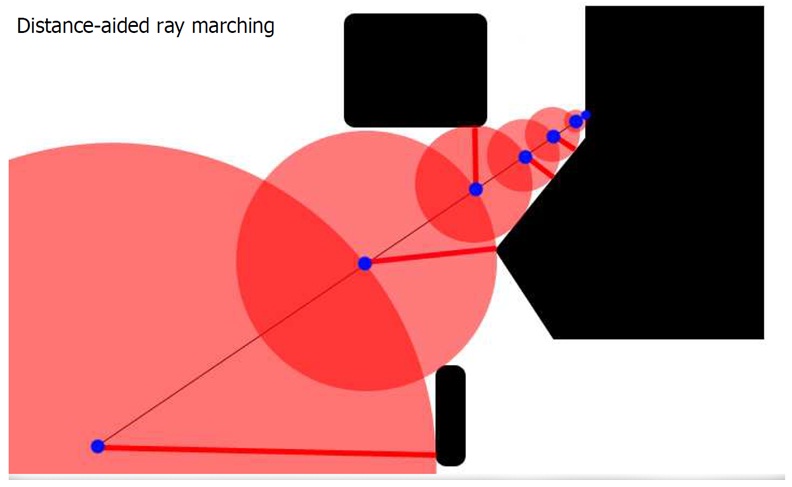
Рисунок 2. Distance-aided ray marching.

Дальше все просто. Мы шагаем по лучу на полученное расстояние и применяем эту процедуру еще раз, до тех пор, пока наше расстояние не станет меньше заданного порога. Следует отметить только, что размер шага было бы хорошо ограничивать снизу некоторой константой, для т.к. в противном случае трассировка будет очень медленной вблизи границ объектов.

Еще одна тонкость, для того чтобы не продолжать реймарчинг до бесконечности, вам необходимо в самом начале найти пересечение луча и ограничивающего всю сцену bounding box-а. Как только вы выходите за этот бокс (t > tmax) – остановить реймарчинг. Либо вы просто можете ограничить максимальное число шагов по лучу какой-либо достаточно большой константой.

Вычисление нормали

Нормаль есть не что иное, как градиент к поверхности. Вычисляем ее численно.

float3 EstimateNormal(float3 z, float eps)

{

       float3 z1 = z + float3(eps, 0, 0);

       float3 z2 = z - float3(eps, 0, 0);

       float3 z3 = z + float3(0, eps, 0);

       float3 z4 = z - float3(0, eps, 0);

       float3 z5 = z + float3(0, 0, eps);

       float3 z6 = z - float3(0, 0, eps);

       float dx = DistanceEvaluation(z1) - DistanceEvaluation(z2);

       float dy = DistanceEvaluation(z3) - DistanceEvaluation(z4);

       float dz = DistanceEvaluation(z5) - DistanceEvaluation(z6);

       return normalize(float3(dx, dy, dz) / (2.0*eps));

}