Андрей Лебедев

История развития алгоритмов глобального освещения. Компьютерная графика и мультимедиа. Выпуск №9(1)/2011. http://cgm.computergraphics.ru/issues/issue19/globalillum Выпуск: Выпуск №9(1)/2011

Алгоритм излучательности рассматривает частный случай решения уравнения освещенности, когда материалы являются диффузными. Материал называется диффузным, если вся энергия, отраженная от его поверхности рассеивается равномерно по всем направлениям [16]. ДФО диффузных материалов равняется константе, поэтому интеграл в уравнении освещенности принимает более простой вид. На практике материалы далеко не всегда являются диффузными, возможен случай существования нескольких максимумов ДФО (в англоязычной литературе такие материалы называются glossy materials – см. Рис. [1]).

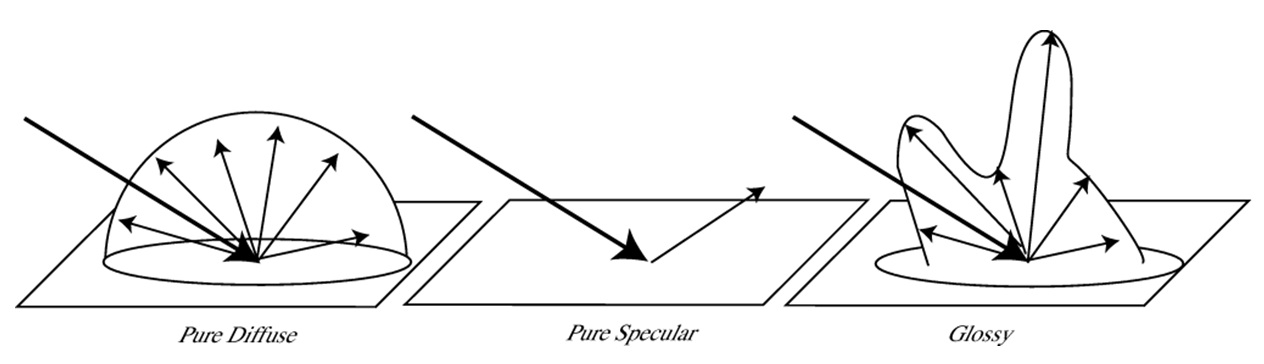
 Рис. 1. Различные модели ДФО.

Другим важным ограничением является требование замкнутости системы, т.е. суммарная энергия в системе должна сохраняться (что, вообще говоря, обязательно в уравнении освещенности). Поэтому если Вам необходимо смоделировать сцену, где все материалы заданы при помощи модели Фонга [10], то алгоритм излучательности не подойдет по двум причинам. Первая – в общем случае материалы не будут диффузными. Вторая – модель Фонга не сохраняет энергию. Перейдем к рассмотрению классической схемы метода излучательности.

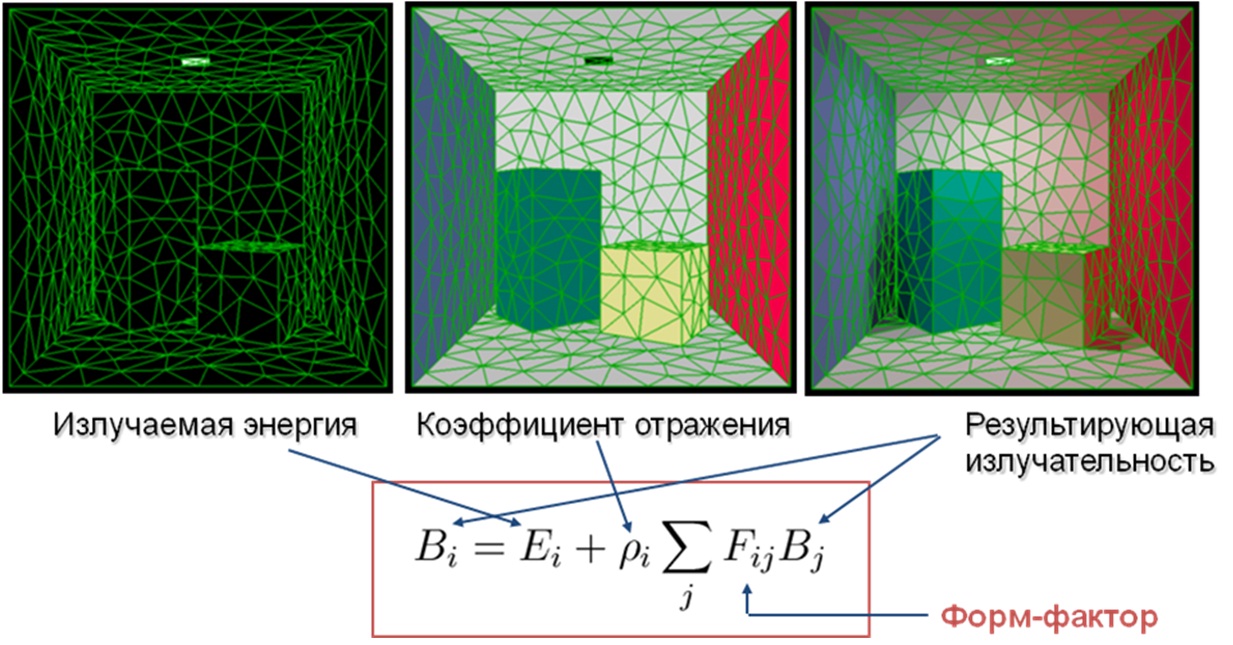
На первом этапе алгоритма все поверхности сцены делятся на патчи. Патч – это элементарная единица поверхности. Дискретизация поверхности на патчи позволяет заменить интеграл в уравнении освещенности на конечную сумму интегралов специального вида. Каждый такой интеграл, называемый форм-фактором, задает взаимное влияние двух отдельных патчей (т.е. сколько энергии переходит от одного патча к другому). Если мы знаем значение каждого форм-фактора (для каждой пары патчей), то процесс синтеза изображений сводится к решению системы линейных алгебраических уравнений. Основная трудность в алгоритме – расчет форм-факторов. Далее приведены некоторые математические выкладки, подкрепляющие словесное описание алгоритма.

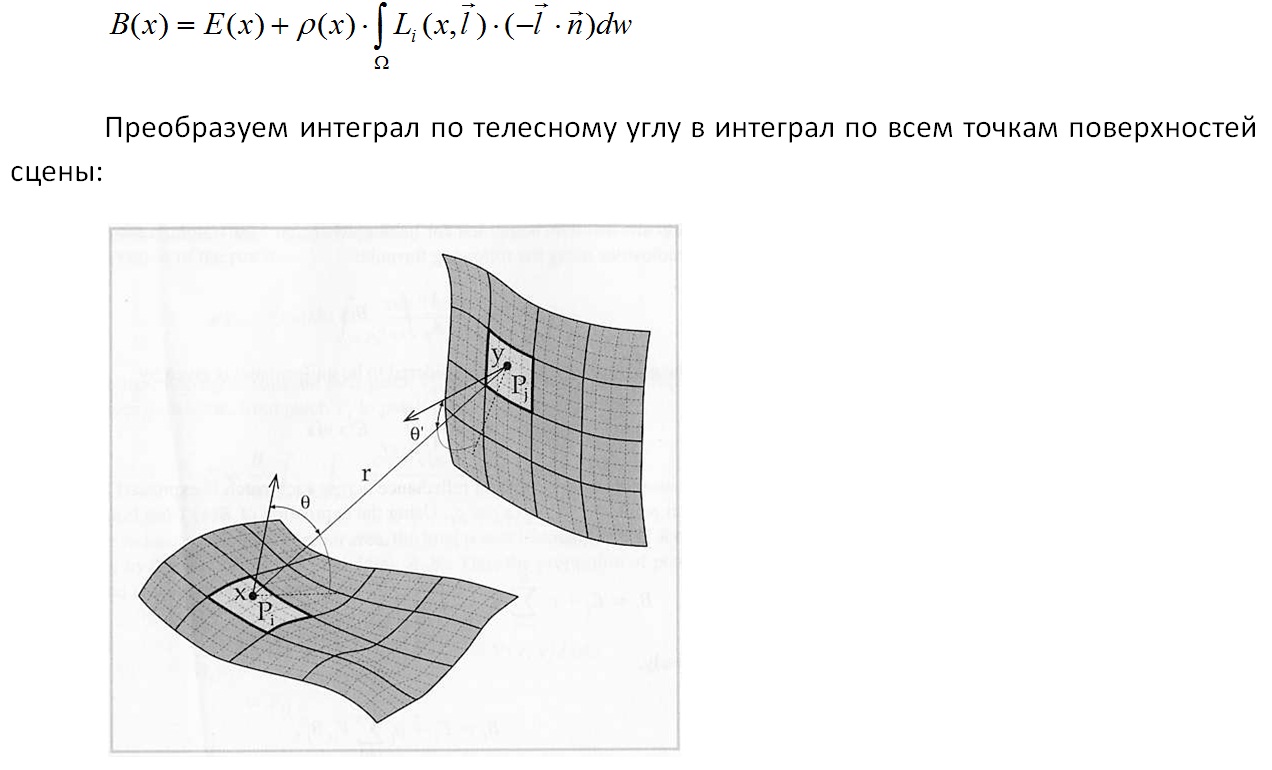
Как было упомянуто выше, для алгоритма излучательности необходим метод расчета форм-фактора. Для начала рассмотрим алгоритм полукуба (hemicube algorithm [17]). Алгоритм основан на т.н. аналогии Нуссельта (см. Рис.2). Согласно этой аналогии форм-фактор можно рассчитать чисто геометрическим способом. Рассмотрим некоторый дифференциальный патч (элемент разбиения патча) и некоторую сферу с центром в этом патче. Возьмем теперь второй патч, от которого мы будем рассчитывать форм-фактор, и спроецируем его на эту сферу. Полученную проекцию спроецируем на плоскость первого патча и поделим на площадь окружности. Проведя эти действия для всех дифференциальных патчей, и просуммировав результаты, мы получим значение форм-фактора. В алгоритме полукуба для ускорения расчета проекции патча на сферу, сфера заменяется на аппроксимирующий ее куб (см. Рис. 3). Это позволяет существенно повысить скорость алгоритма на имеющейся аппаратуре, однако иногда при этом страдает и качество (см. Рис. 3).

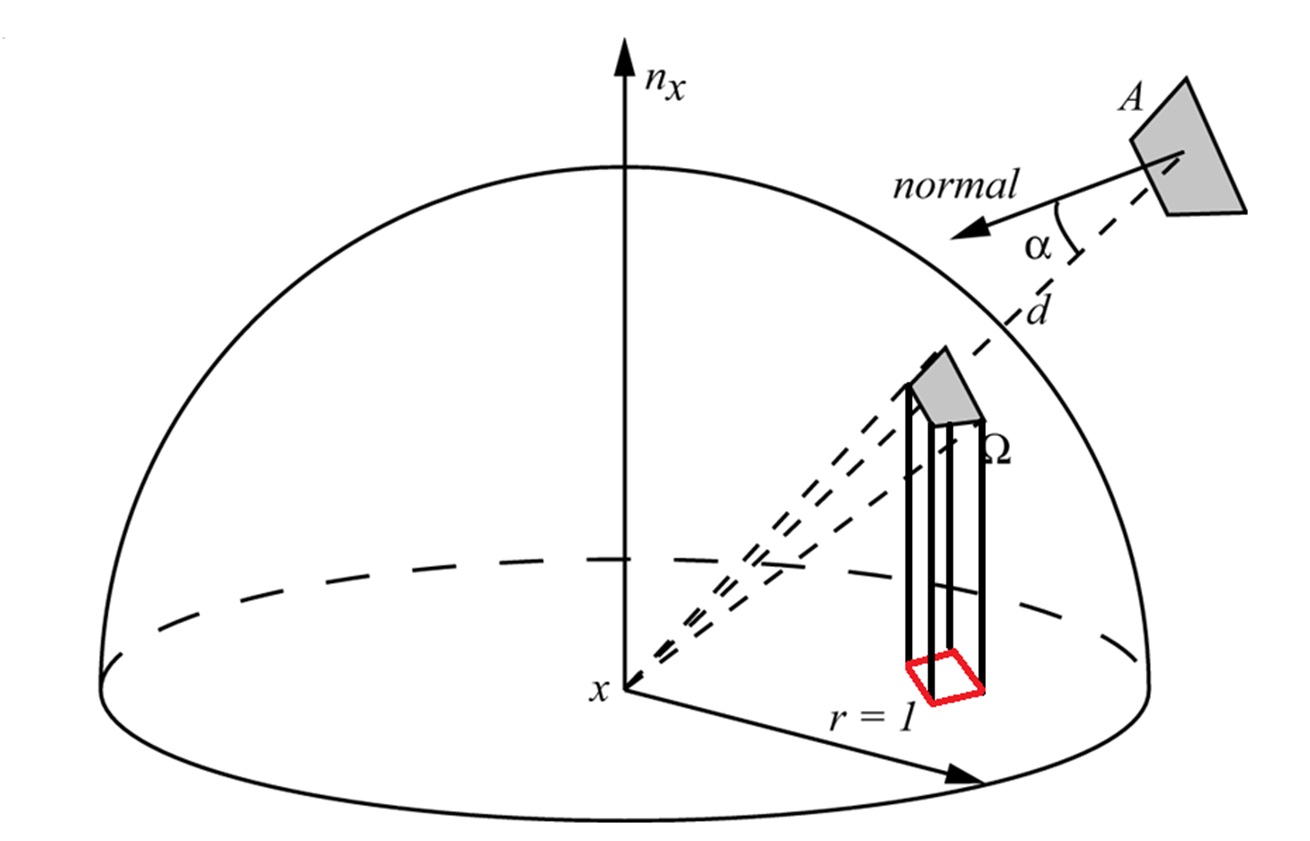
Рис. 2. Аналогия Нуссельта [1] (красным помечена область, площадь которой численно равна форм-фактору дифференциального патча и патча A).

Рис. 3. Аппроксимация сферы кубом в разрезе (слева) и возникающие при этом артефакты (справа [51]).

Для того чтобы решить проблему полукуба Волтон [18] предложил метод расчета форм-факторов на основе трассировки лучей. Один из патчей принимается за источник света (площадный), а второй патч выступает в качестве поверхности–приемника лучей. Площадь патча-источника подразбивается на более мелкие независимые патчи (фактически это дифференциальные патчи). Из каждого подпатча испускаются лучи. При увеличении числа лучей точность расчета форм-фактора увеличивается. Обычно процесс испускания лучей заканчивается, когда значение форм-фактора практически перестает изменяться. Рассмотренный алгоритм дает намного лучшие результаты, чем метод полукуба, ценой более высокой вычислительной сложности. Этот алгоритм еще интересен тем, что в нем используется интересный прием отождествления отражающей поверхности с новым источником света. Позднее этот прием применяется в алгоритме Lightcut для расчета вторичного освещения (см. п.6).

Существуют и гибридные методы для расчета форм-фактора, которые ликвидируют недостатки метода полукуба и работают быстрее метода трассировки [19].

На последнем этапе метода излучательности происходит решение системы линейных алгебраических уравнений. Обычно решение ищется каким-то из итерационных методов (например, методом Зейделя [20]), т.к. сложность таких методов на порядок ниже, чем у прямых (N² по сравнению с N³).

Примеры визуализации методом излучательности приведены на Рис. 4. Стоит отметить еще один недостаток алгоритма – сложность моделирования мягких теней, т.е. теней от протяженных источников. При моделировании мягких теней возникают т.н. блочные тени. Блочные тени образуются из-за того, что минимальной единицей расчета освещения является патч. Единственный способ побороться с подобными артефактами – произвести подразбиение патчей в области мягкой тени.

Рис. 5. Результаты метода излучения (справа особенно заметна проблема блочных теней) [50, 51].

Литература

[16] Kerker, M. The Scattering of Light. New York: Academic, 1969. 666 p.

[17] Cohen M., GreenBurg D. The Hemi-cube: A Radiosity solution for complex it is hard to achieve environments // Proceedings of SIGGRAPH’85 in Computer Graphics, 1985. 19. N 3. P. 31-40.

[18] Walton G. Calculation of Obstructed View Factors by Adaptive Integration, NIST Report NISTIR-6925 [PDF] (http://www.bfrl.nist.gov/IAQanalysis/docs/NISTIR-6925.pdf)

[19] Baum D., Rushmeier H., Winget J. Improving Radiosity Solutions Through the use of Analytically Determined Form-Factors // Proceedings of SIGGRAPH89 In Computer Graphics, 1989. 23. N 3. P. 325-334.

[20] Gauss - Seidel method. [HTML] http://en.wikipedia.org/wiki/Gauss%E2%80%93Seidel_method