|
Все 3D пространство разбивается на мелкую регулярную сетку, состоящую из N*N*N кубиков. Идея заключается в том, что можно пробегать только по тем по кубикам, через которые пошел луч. Это можно сделать по-разному.
1) Алгоритм Брезенхема в 3D.
Откровенно говоря, это дурацкая идея. Дело в том, что луч изначально задан с float точностью, однако в алгоритме брезенхема используются целочисленные координаты. Поэтому сущетсвует вероятность того, что луч промахнется относительно некоторых кубиков, потому что в алгоритме брезенхема бегает на самом деле не тот луч, который мы в действительности трассируем, а некоторое его приближение. Чем больше кубиков в сетке, тем это приближение точнее и вероятность промаха меньше, но тем медленнее работает траверс.
Исходники алгоритмома брезенхема в 3D на C++ можно скачать по следующей ссылке. http://ray-tracing.ru/upload/free/Bresenham3D_14nov2007.rar
Исходники трассировщика, использующего регулярную сетку и алгоритм брезенхема в 3D.
http://ray-tracing.ru/upload/free/TEST_MODEL_ENGINE6.rar
(нажмите F2 для включения попиксельной трассировки)
2) Алгоритм 3DDA (модификация алгоритма Fujimoto)
Этот алгоритм аккуратно обходит все кубики в сетке, используя координаты с плавающей точкой. На этот раз, кубики можно делать довольно большими не опасаясь того, что луч промахнется мимо каких-то треугольников. Идея примерно та же, что и в алгоритме Брезенхема. Алгоритм можно разделить на два этапа. Инициализация и собственно сам траверс. Инициализация довольно сложная, но зато после того, как для луча один раз она выполнена, сам цикл прослеживания луча становится очень простым.
Рассмотрим сначала 2D вариант.
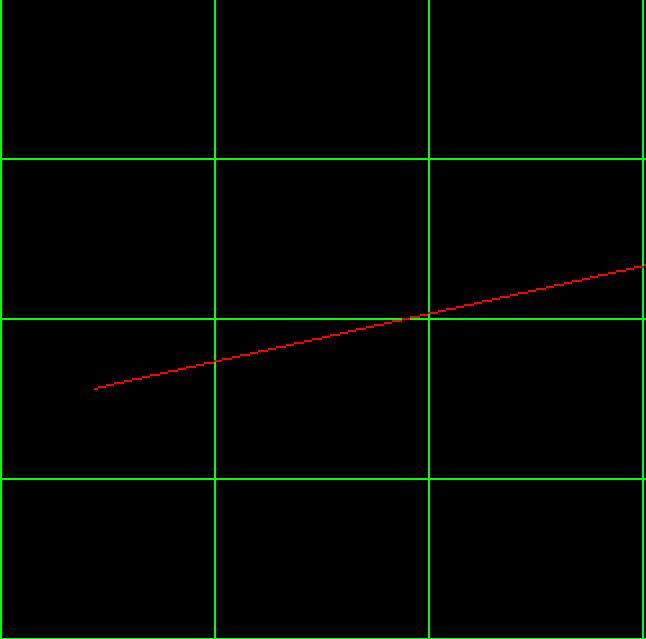 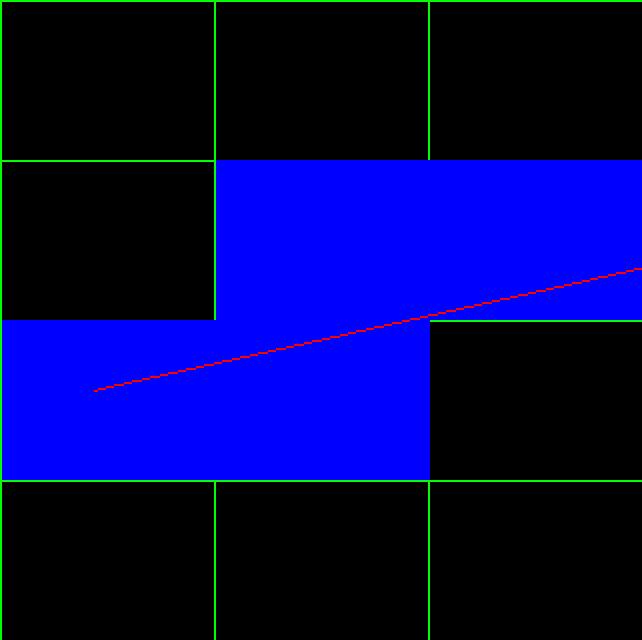
Рисунок 1. результат работы алгоритма для заданного луча
1) Нужно посчитать пересечение луча и ограничивающего всю сцену бокса и сохранить первую точку удара как t_min (параметрическое уравнение прямой). Если t_min меньше нуля, то берем origin луча.
if(!IntersectRay2fBox2f(ray, box, t_min)) // вообще-то передават t_min по ссылке это зло
return;
if(t_min < 0)
t_min = 0;
2) Вычислим 2 координаты (декартовы) точки пересечения луча и бокса. Если t_min = 0, то получится origin луча.
float startX = ray.pos.x() + t_min*ray.dir.x();
float startY = ray.pos.y() + t_min*ray.dir.y();
3) Вычислим номера начального воксела, в который попал луч. CELL_NUMBER - это размер сетки (всего вокселов CELL_NUMBER*CELL_NUMBER). Для простоты примем это число за константу.
int x = (int)((startX - box.vmin.x())/(box.vmax.x() - box.vmin.x())*CELL_NUMBER);
int y = (int)((startY - box.vmin.y())/(box.vmax.y() - box.vmin.y())*CELL_NUMBER);
if(x == CELL_NUMBER) x--;
if(y == CELL_NUMBER) y--;
4) Теперь нам нужно найти две крайние координаты вокселей, в стенки которых упрется луч (voxelMaxX и voxelMaxY). Они позволят нам рассчитать начальные значения tMaxX и tMaxY - координат в (пространстве луча) пересечения лучем двух ближайших плоскостей сетки (с.м. рисунок 2). На этом шаге мы также рассчитаем будущее приращение к целочисленным координатам x и y, которые как и крайние координаты зависят от знака направления луча (stepX и stepY).
vec2f boxSize = box.vmax - box.vmin;
float tVoxelX, tVoxelY;
int stepX, stepY;
if(ray.dir.x() >= 0) // в 3D случае важно именно >= 0 а не > 0
{
tVoxelX = ( float)(x+1)/(float)CELL_NUMBER;
stepX = 1;
}
else
{
tVoxelX = ( float)x/(float)CELL_NUMBER;
stepX = -1;
}
if(ray.dir.y() >= 0)
{
tVoxelY = ( float)(y+1)/(float)CELL_NUMBER;
stepY = 1;
}
else
{
tVoxelY = ( float)y/(float)CELL_NUMBER;
stepY = -1;
}
float voxelMaxX = box.vmin.x() + tVoxelX*boxSize.x();
float voxelMaxY = box.vmin.y() + tVoxelY*boxSize.y();
float tMaxX = t_min + (voxelMaxX - startX)/ray.dir.x();
float tMaxY = t_min + (voxelMaxY - startY)/ray.dir.y();
5) Рассчитаем приращения с плавающей точкой по x и по y, которые мы будем делать на каждом шаге алгоритма.
const float voxelSize = (box.vmax.x() - box.vmin.x())/CELL_NUMBER;
const float tDeltaX = voxelSize/fabs(ray.dir.x());
const float tDeltaY = voxelSize/fabs(ray.dir.y());
6) Ну и последнее, собственно алгоритм 2DDA. Как видно, он очень прост.
while(x < CELL_NUMBER && x >= 0 && y < CELL_NUMBER && y >= 0)
{
NextVoxel(x, y, box); // box передается только чтобы нарисовать воксель, так он не нужен
if(tMaxX < tMaxY)
{
tMaxX += tDeltaX;
x += stepX;
}
else
{
tMaxY += tDeltaY;
y += stepY;
}
};
Реализацию двухмерного алгоритма с визуализацией можно скачать по следующей ссылке (файл FujimotoTraverse.cpp): http://ray-tracing.ru/upload/sources/Fujimoto2D_28_February_2009.zip
Управление: мышкой вправо влево -вращать луч, WASD - двигать.
Отдельно алгоритм выложен здесь: http://ray-tracing.ru/upload/sources/FujimotoTrav.rar
Здесь верcия 2DDA на C# http://www.ray-tracing.ru/upload/sources/fujimoto2D.cs от 'wishmaster35'.
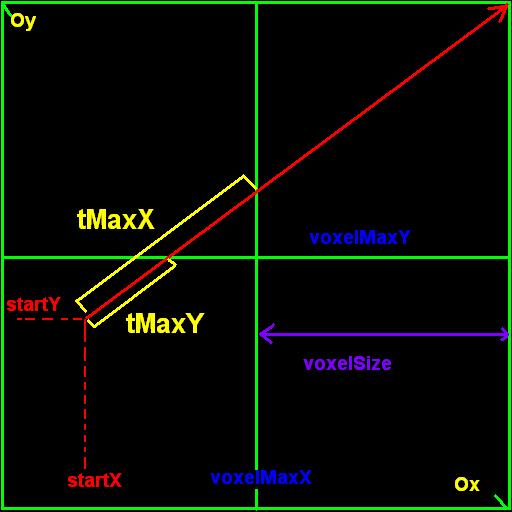
Рисунок 2. Алгоритм 2DDA.
3DDA алгоритм выглядит не сильно сложнее чем 2DDA.
Основной модификации подвергнется ядро алгоритма - цикл перебора вокселей. Как видим, модификеация совсем не сложная.
if(tMaxX <= tMaxY && tMaxX <= tMaxZ)
{
tMaxX += tDeltaX;
x += stepX;
}
else if(tMaxY <= tMaxZ && tMaxY <= tMaxX)
{
tMaxY += tDeltaY;
y += stepY;
}
else
{
tMaxZ += tDeltaZ;
z += stepZ;
}
Проблема повторных пересечений
Регулярная сетка неадаптивна. И дело здесь не только в том, что на пустое пространство тратится много кубиков. Еще одна проблема для регулярной сетки - разный размер примитивов. Одни треугольники могут быть очень большими, другие - очень маленькими. Но размер разбиения должен быть выбран один и тот же. Если выбрать размер кубика большим, то неэффективно будут обходиться сложные регионы. Поэтому, размер обычно стараются выбрать поменьше. В случае если в сцене существуют примитивы размер которых сильно больше, чем размер кубиков, луч может посчитать пересечение с одним и тем же примитивом очень много раз. Конечно, эта проблема встречается во всех ускоряющих структурах, но в регулярной сетке она наиболее заметна. Для того чтобы не считать повторные пересечения, обычно в примитивах сохраняют индекс последнего луча, с которым считалось пересечение. Если индекс в примитиве и индекс луча равны, пересечение считать ненужно. На рис. 3 луч может посчитать пересечение с одним и тем же треугольником 7 раз, прежде чем выйдет за пределы сетки.
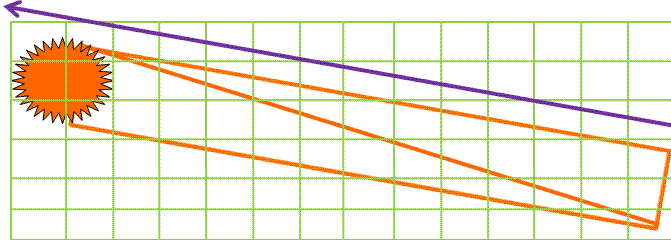
Рисунок 3. Проблема повторных пересечений
Достоинства регулярной сетки
- Хорошая скорость на сложных участках.
- Простота. Возможна аппаратная реализация.
- Просто и быстро строится.
Проблемы регулярной сетки
-
Неадаптивна. Проблема чайника на стадионе. Алгоритм поиска очень хорошо работает для сложных, заполненных сцен. Однако с пустыми пространствами он справляется плохо, работая фактически в холостую.
-
Требовательна по памяти
-
Проблема повторных пересечений
Заключение
Регулярная сетка очень плохо подходит для ускорения трассировки лучей. Хуже всего что алгоритм неадаптивен и для реальных задач сетка совершенно бесполезна. В целом, чем более нерегулярна структура, тем лучше она для рейтрейсинга, так как позволяет на каждом шаге выбрать наилучшее разбиение. kd и BVH дереья очень хорошо справляются с ускорением трассировки лучей. Регулярные, иерархические сетки и октодереьвья не годяться. |