скачать алгоритм можно отсюда

http://ray-tracing.ru/upload/sources/packet_kd_tree_trav.cpp

Введение

Посмотрим что такое packet tracing или трассировка пакетов. На самом деле мы рассмотрим kd tree packet traversal (прослеживание или поиск в kd дереве пакетами лучей) - это один из основных этапов пакетной трассировки. Следует упомянуть, что помимо пакетной еще существует групповая трассировка. И в том и в другом случаях берется некая группа лучей. В англоязычной литературе присутствует великая путаница по этому поводу, все все называют по-разному - packet tracing, beam tracing, но не разделяют трассировку пакетами и группами.

Групповая трассировка

    В случае групповой трассировки группа лучей ограничивается некоторой фигурой - обычно frustum пирамидой и при поиске учитывается сначала эта ограничивающая фигура. Например пусть у нас есть 4 луча и 10 сфер (нет ускоряющих структур). В случае пакетной трассировки мы просто пересекаем 4 луча одновременно (скажем на SSE) с каждой сферой. А в случае групповой, мы выберем ограничивающую пирамиду, посчитаем сначала пересечение этой пирамиды с каждой сферой, и будем считать пересечение лучей только с теми сферами, с которыми пересекается эта пирамида. То есть выигрыш заключается в том, что если сфера и пирамида не пересекаются, то вообще не нужно проверять лучи в группе. Однако, если пирамида пересекает сферу, мы обязаны проверить все лучи в группе. Групповая трассировка намного эффективнее пакетной в случаях, когда возможна ее реализация и нет сильных расхождений в пакете. Обычно размер групп большой - например по 64-128 лучей или даже больше.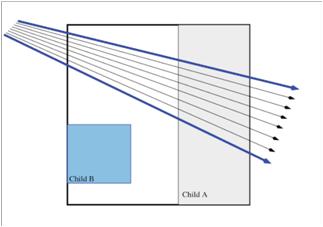

Рисунок 1. групповая трассировка (BVH).

На рисунке 1 показан пример группового поиска в BVH дереве. Сначала проверяется некая фигура, ограничивающая все лучи на пересечение с узлами A и B. Так как узел B не пересекается с этой фигурой, то нет смысла и проверять лучи на пересечение с узлом B.

Пакетная трассировка

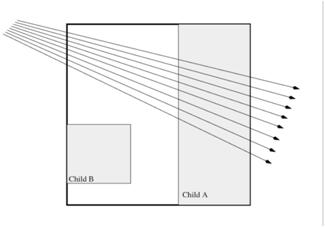
Рисунок 2. Пакетная трассировка (BVH).

    Размер пакетов же, намного меньше - обычно 4 луча в пакете, хотя может быть и больше. Во время поиска пересечений все лучи из пакета обязаны пересечь все объекты, буть то треугольники, сферы или плоскость в kd дереве. Сразу возникает вопрос - так в чем же выигрыш? Ведь мы все-равно считаем столько-же пересечений. На ум сразу приходят SSE инструкции современных процессоров - неудачная попытка. На самом деле краеугольный камень не в них. Конечно, в случае подсчета пересечений методом грубой силы так оно и есть, но вот что касается поиска в kd дереве, соль в другом. Даже если не использовать SSE инструкции, ускорение при поиске в kd дереве будет очень существенным (особенно если kd дерево неоптимально построено). Все дело в том, что пакетная трассировка сокращает количество обращений к памяти при поиске в дереве. Ровно во стольок раз, сколько лучей в пакете. Поэтому нет ничего удивительного в том, что ускорение наблюдается в 3.7-3.9 раз. Правда, если размер пакета большой, лучи в начинают расходиться и эффективность может упасть, так как даже если один луч остановился в каком-то месте, остальные обязаны его подождать. Вообще, размер пакета должен быть регулируемой величиной. Мы рассмотрим трасcировку пакетов с размером 4, как сделано в интеловской статье [1].

Внимание: Алгоритм представленный здесь корректно работает толко если знаки у направлений лучей всего пакета совпадают. Если это не так, нужно использовать обычный траверс. На деле таких лучей мало. Если камера смотрит по оси z, это пикселы на центральных линиях экрана - вертикальной и горизонтальной.

packet kd-tree traversal

    Рассмотрим пакетный поиск по 4 луча. На самом деле идея его практически не отличается от обычного поиска в kd дереве. Сперва выполняем некоторую инициализацию - пересекаем все 4 луча с ограничивающим сцену боксом, инициализируем t_far, t_near. Что-то еще считаем. Нам понанобятся следующие структуры:

struct RayPacket

{

    union { float ox[4]; __m128 ox4; };

    union { float oy[4]; __m128 oy4; };

    union { float oz[4]; __m128 oz4; };

    union { float dx[4]; __m128 dx4; };

    union { float dy[4]; __m128 dy4; };

    union { float dz[4]; __m128 dz4; };

};

// и

struct Packet_Traversal_Data
{
  vec4f  t_far; //  vec4f - некий класс вектора из MGML. Неявно приводится к __m128!
  __m128 mask;
  unsigned int nodeOffset;
};

И еще нам потребуется маска. С помощью нее мы будем помечать, какие лучи активны а какие нет. 0xFFFFFFFF - луч активен. 0 - неактивен.

register __m128 mask;
mask.m128_u32[0] = 0xFFFFFFFF;
mask.m128_u32[1] = 0xFFFFFFFF;
mask.m128_u32[2] = 0xFFFFFFFF;
mask.m128_u32[3] = 0xFFFFFFFF;

Поначалу все лучи активны. Мы траверсим лучи сквозь kd-дерево. Когда какие-то из них пересекаются с геометрией, мы помечаем их как неактивные и продолжаем траверсить пакет до тех пор пока все лучи не найдут пересечение. Маска также может стать нулевой при попадание лучей одного пакета в разные узлы, поэтому если в ней все 4 нуля это еще не означает что траверс окончен.

Смотрим на основной цикл.

Если все 4 луча попали в дальний узел, идем в дальний.

//if all t_split[0..3] < t_near[0..3] where mask = '0xFFFFFFFF' then all rays in far node

//
if (_mm_movemask_ps( _mm_and_ps( _mm_cmplt_ps( t_split, t_near ), mask ))  == _mm_movemask_ps(mask) )
{
    node = kd_tree->GetNodeByOffset(farNodeOffset);
}

Иначе если все четыре луча попали в ближний узел, идем в ближний.

// else if all t_split[0..3] > t_far[0..3] where mask = '0xFFFFFFFF' then all rays in near node

//
else if(_mm_movemask_ps( _mm_and_ps( _mm_cmpge_ps( t_split, t_far ), mask )) ==  _mm_movemask_ps(mask) )
{
  node = kd_tree->GetNodeByOffset(nearNodeOffset);
}

В противном случае, мы поступаем так: для тех лучей, которые попали в ближний узел, оставляем маску такую как и была и идем в ближний узел, не забывая поместить в стек старую маску, чтобы восстановить состояние лучей, при подъеме из листьев kd дерева. Для лучей, которые не попали в ближайший узел ставим маску в 0.

else
{
  node = kd_tree->GetNodeByOffset(nearNodeOffset);

  // stack.push( node->far, t_far[0..3], mask[0..3] )
  m_Stack[top].nodeOffset = farNodeOffset;
  m_Stack[top].t_far  = t_far;
  m_Stack[top].mask  = mask;
  top++;
 
  // needn't use mask there, we will repair t_far when pop far node from stack
  t_far = t_split;
  // go to the nearest node, traverse rays where t_split[0..3] > t_near[0..3]
  mask  = _mm_and_ps(mask,_mm_cmpgt_ps( t_split, t_near ));
}

При выходе из внутреннего цикла мы попадаем в лист (while (!node.Leaf())). Считаем пересечения со всеми треугольниками в листие (можно пакетами, можно без пакетов).

// compute intersections, store result 't' in t_hit if intersects
vec4f t_hit = infinity;
for (int i=0;i<4;i++)
{
  if (mask.m128_u32[i])
    t_hit[i] = IntersectAllPrimitivesInLeaf(ray_packet.GetRay(i),node,pHits+i);
}

Ну а теперь делаем проверки, не остановить ли нам поиск, достаем из стека все необходимые значения. И продолжаем траверсить дерево.

// store trav_result where t_hit[0..3] <= t_far[0..3]
trav_result = _mm_or_ps(trav_result,_mm_cmple_ps(t_hit,t_far));

// all 4 rays have been stoped, nothing else to traverse anymore
if (top == 0 || _mm_movemask_ps(trav_result) == 0xF )
   break;

//t_near[0..3] = t_far[0..3] where ray not hit; 
mask = _mm_andnot_ps(trav_result ,mask); 
t_near = _mm_or_ps(_mm_and_ps( mask, t_far),_mm_andnot_ps(mask,t_near));

// (next_node,t_far,mask) = stack.pop();
top--;
nodeOffset  = m_Stack[top].nodeOffset;
t_far  = m_Stack[top].t_far; // btw, here we repair t_far
mask  = _mm_andnot_ps(trav_result ,m_Stack[top].mask);

1. Интерактивная трассировка лучей с использованием SIMD инструкций.