Изображение хранится в памяти как двумерная матрица пикселей. Однако, считается, что изображение предметов реального мира это не просто набор пикселей. Авторы [6] склонны рассматривать изображение как непрерывную двумерную функцию. То, что мы видим на экране – приближение этой функции, ее дискретизованное в заданном разрешение представление. Трассировка лучей в самом общем понимании - это метод, позволяющий восстановить значения этой функции с помощью точечных сэмплов, то есть значений этой функции в точках. В данной работе не рассматриваются вопросы восприятия изображения человеческим глазом, обработка информации мозгом и вопросы фильтрации изображений. Сосредоточимся лишь на том, как получать значения функции изображения в точках.

Каждой точке в двухмерном пространстве экрана соответствует точка на некоторой поверхности (эту точку можно найти с помощью прослеживания пути луча, выпущенного из виртуального глаза через точку экрана в сцену; назовем ее точкой x). Освещенность точке поверхности x вычисляется при помощи интеграла следующего вида [6]:

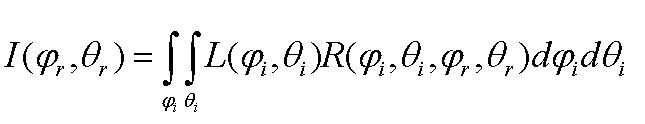
Рисунок 1. Интеграл освещённости.

Вычисляемая интегрированием интенсивность освещения в точке I(φ_r, θ_r) является не числом, а функцией. Другими словами, она дает значения интенсивности света, отражаемой поверхностью под разными углами. Таким образом, выполняя интегрирование по полусфере приходящего (падающего) в точку освещения L c учетом свойств поверхности R, мы получаем новую функцию распределения освещения в пространстве, обусловленную свойствами отражения поверхности (материала) в точке x. Хотя если мы рассматриваем луч, который трассировали через пиксел из виртуального глаза, то направление конечно одно и задано этим лучом.

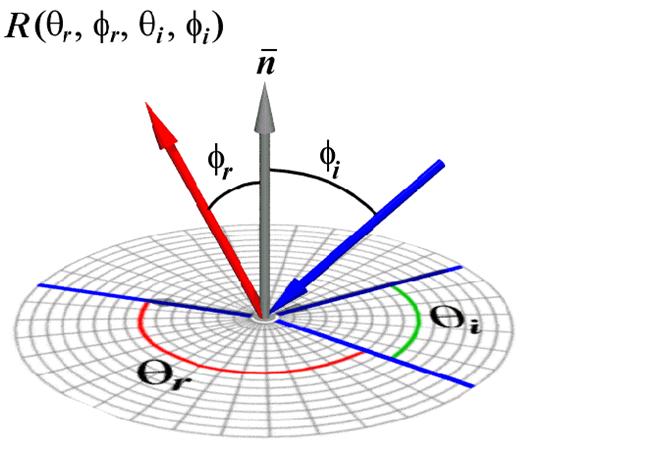
Рисунок 2. Двулучевая Функция Отражательной Способности - ДФО (Bidirectional Reflectance Distribution Function - BRDF).

Формула (рис. 1) берется их тех соображений, что освещенность в точке поверхности складывается из света, падающего на поверхность со всех направлений и отражающегося по какому-то определенному закону (какому именно, устанавливает функция ДФО). Эта формула не более чем математическая модель и она верна не всегда. Например, в случае стекла нужно учитывать свет, приходящий из под поверхности и проводить интегрирование по полной сфере. В случае кожи ситуация еще сложнее, так как необходимо учитывать такой эффект как подповерхностное рассеивание.

Существуют различные способы вычисления интеграла на рис. 7. Одни из них более точные, другие менее точные, но более быстрые. Рассмотрим их по порядку.

Ссылки

[6] Pharr, M. and Humphreys, G. 2004 Physically Based Rendering: from Theory to Implementation. Morgan Kaufmann Publishers Inc.

В рассмотренных алгоритмах вычисление пути света начиналось всегда с обратной стороны, то есть из виртуального глаза. Но существуют алгоритмы, где прослеживание пути световых лучей ведется из источника света, или с обеих сторон. Наиболее совершенным из них считается алгоритм “Metropolis light transport”. Идея этого алгоритма чем-то похожа на идею генетических алгоритмов. Для каждого пиксела и источника света алгоритм выбирает некий случайный начальный путь X₀, по которому свет может дойти от источника света до глаза. Затем, генерируется последовательность путей X₀X_1.. X_n. В этой последовательности каждый следующий путь получен из предыдущего с помощью случайных мутаций. При этом, мутации могут приниматься или отвергаться – в зависимости от того какой вклад вносит результирующий путь X_i+1 в изображение по сравнению с X_i.

На рис. 1. функция AcceptProb(Y|X) является оценочной функцией и говорит, насколько хорош новый путь относительно старого пути x.