Введем следующие обозначения: P - origin луча, v - его направление. v0,v1,v2 - вершины треугольника. z - точка пересечения. t - расстояние от точки вылета луча до точки пересечения луча и треугольника. u,v,t1 - барицентрические координаты. Барицентрические координаты представляют собой отношения площадей маленьких треугольников к большому треугольнику. (рис. 1.)

x u := u/S, v := v/S, t1 := t1/S

x t1 = 1 – u - v

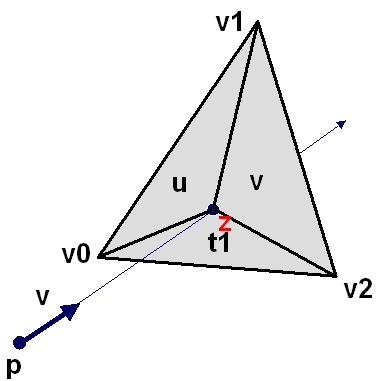
Рис. 1. пересечение луча и треугольника

Барицентрический тест (fast minimal storage ray triangle intersection)

Это самый известный тест на пересечение «луч-треугольник». Имея 3 точки на плоскости, можно выразить любую другую точку через ее барицентричечкие координаты. Первое уравнение берется просто из определения барицентрических координат, выражая точку пересечения z. С другой стороны, эта же точка z лежит на прямой. Второе уравнение таким образом, это просто параметрическое уравнение прямой. Прировняв правые части уравнений 1 и 2 получаем третье уравнение, которое, по сути, является системой 3-х уравнений (p,v,v1,v2,v3 - векторы) с 3-мя неизвестными (u,v,t).

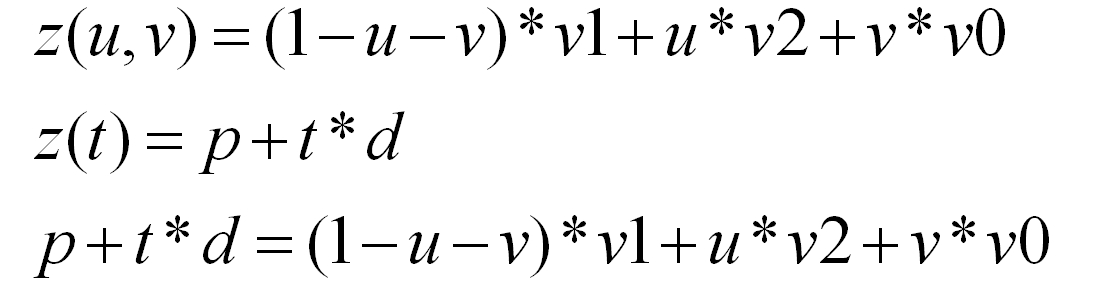
 Проведя алгебраические преобразования получим ответ в следующем виде:

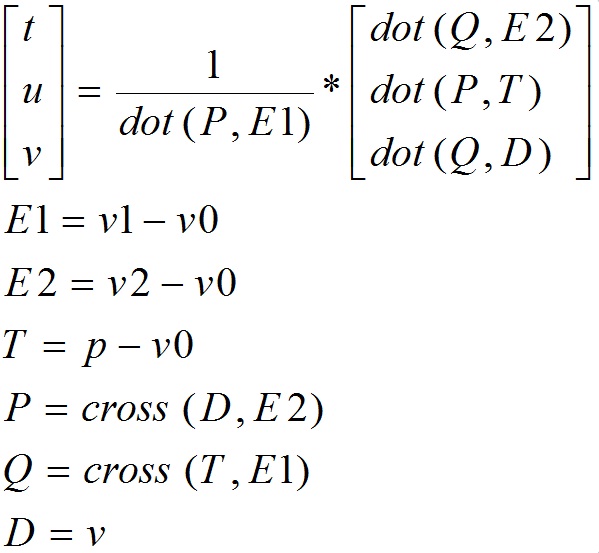
Юнит тест (Woop's unit test)

Основная идея данного алгоритма заключается в том, чтобы посчитать матрицу преобразования треугольника в некий единичный треугольник (отсюда название) с вершинами (1,0,0); (0,1,0); (0,0,0).  Во время подсчета пересечения луч преобразуется этой матрицей в пространство, где треугольник имеет единичное представление. После преобразования вычислить пересечение намного проще, так как нужно считать пересечение с заранее известным треугольником (1,0,0); (0,1,0); (0,0,0). Пусть задан треугольник с вершинами A,B,C.

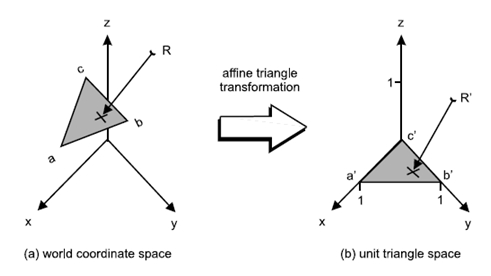
Рис. 3. Афинное преобразование треугольника в пространство, где он имеет единичное представление.

Рассмотрим преобразование T_∆^-1:

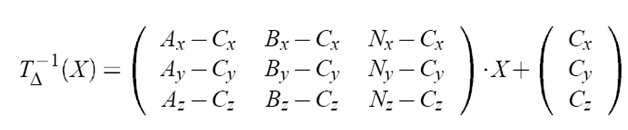
Если применить данное преобразование к треугольнику (1,0,0); (0,1,0); (0,0,0); то получим исходный треугольник.

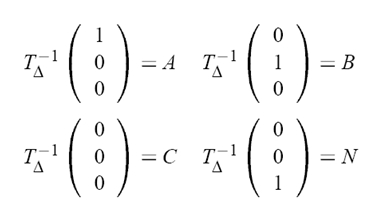
Для того чтобы найти нужное нам преобразование необходимо дополнить матрицу T∆-1 до 4x4 (добавить еще одну строчку (0,0,0,1)) и найти обратную матрицу. Это будет соответствовать обратному T∆-1 преобразованию. После, необходимо лишь умножить луч на полученную матрицу и посчитать пересечение с единичным треугольником.

float3 o = mul3x4(m, ray_origin);

float3 d = mul3x3(m, ray_direction);

float t = -o.z/d.z;

float u = o.x + t*d.x;

float v = o.y + t*d.y;

Функция mul3x4 выполняет умножение подматрицы 3x3 на трехмерный вектор и добавляет к результату последний столбец (3 его компоненты). Функция mul3x3 просто умножает подматрицу 3x3 на трехмерный вектор.

Немного об эффективности

Несмотря на то, что юнит-тест делает немного меньше вычислений (в худшем случае), с алгоритмической точки зрения он менее эффективен. Причина заключается в том, что в юнит-тесте сначала вычисляется координата t, а потом уже u и v. Как правило, если в сцене много мелких треугольников, именно по координатам u и v можно быстро отбросить те треугольники, которые заведомо не пересекаются.

Основное достоинства юнит-теста заключается в том, что он более экономно расходует регистры графического процессора при реализации алгоритма на GPU и его проще реализовать в железе (например на FPGA).