Рассмотрим структуру бинарного пространственного разбиения, называемая kd-дерево. Эта структура представляет собой бинарное дерево ограничивающих параллелепипедов, вложенных друг в друга. Каждый параллелепипед в kd-дереве разбивается плоскостью, перпендикулярной одной из осей координат на два дочерних параллелепипеда.

Вся сцена целиком содержится внутри корневого параллелепипеда, но, продолжая рекурсивное разбиение параллелепипедов, можно прийти к тому, что в каждом листовом параллелепипеде будет содержаться лишь небольшое число примитивов. Таким образом, kd-дерево позволяет использовать бинарный поиск для нахождения примитива, пересекаемого лучом.

Построение kd-дерева

Алгоритм построения kd-дерева можно представить следующим образом (будем называть прямоугольный параллелепипед англоязычным словом "бокс" (box) ).  

1. "Добавить" все примитивы в ограничивающий бокс. Т.е построить ограничивающий все примитивы бокс, который будет соответствовать корневому узлу дерева.
2. Если примитивов в узле мало или достигнут предел глубины дерева, завершить построение.
3. Выбрать плоскость разбиения, которая делит данный узел на два дочерних. Будем называть их правым и левым узлами дерева.
4. Добавить примитивы, пересекающиеся с боксом левого узла в левый узел, примитивы, пересекающиеся с боксом правого узла в правый.
5. Для каждого из узлов рекурсивно выполнить данный алгоритм начиная с шага 2.

Самым сложным в построении kd-дерева является 3-ий шаг. От него напрямую зависит эффективность ускоряющей структуры. Существует несколько способов выбора плоскости разбиения, рассмотрим их по порядку.

1. Выбрать плоскость разбиения по центру.

Самый простой способ - выбирать плоскость по центру бокса. Сначала выбираем ось (x, y или z), в которой бокс имеет макимальный размер, затем разбиваем бокс по центру.

    Рисунок 1: Разбиение по центру

Этот способ имеет плохую адаптивность. Классическое октодерево имеет те же недостатки. Интуитивно можно описать причину плохой скорости на таких деревьях тем, что в каждом узле достаточно много пустого пространства, через которое луч траверсится (проходи через дерево во время поиска) в то время как пустое пространство должно сразу-же по-возможности отбрасываться. Более строгое объяснение будет дано чуть позже.

2. Выбрать плоскость по медиане.

Можно подумать, что было бы неплохо разделять узел на два дочерних каждый раз так, чтобы в правом и левом поддереве количество примитивов было одинаково. Таким образом мы построим сбалансированное дерево, что должно ускорить поиск.

Рисунок 2: Разбиение по медиане

Это не очень удачная идея. Все дело в том, что сбалансированные деревья могут помочь только если искомый элемент каждый раз находится в случайном узле, то есть если распределение лучей по узлам во время поиска будет равномерно. В действительности, это не так. Лучей в среднем пойдет больше в тот узел, который больше по своей площади поверхности, а при медианном разбиении эти площади у узлов могут быть разные.

3. Surface Area Heuristic (SAH)

Каковы же критерии хорошо-построенного kd-дерева? На интуитивном уровне это на самом деле это не очень понятно, хотя выражение "как можно больше пустого пространство должно быть отброшено как можно быстрее" наверное подойдет.

Используем формальный подход. Введем функцию стоимости прослеживания (cost traversal), которая будет отражать, насколько дорого по вычислительным ресурсам прослеживать данный узел случайным набором лучей. Будем вычислять ее по следующей формуле.

SAH(x) = CostEmpty + SurfaceArea(Left)*N(Left) + SurfaceArea(Right)*N(Right)

Где  CostEmpty -  стоимость прослеживания пустого узла (некоторая константа), SurfaceArea - площадь поверхности соответствующего узла, а N - число примитивов в нем. Нужно выбирать плоскость разбиениея так, чтобы минимизировать эту функцию. Аргумент функции x является одномерной координатой плоскости разбиения.

Хорошими кандидатами на минимум SAH могут служить границы примитивов. Простой алгоритм посторения выглядит следующим образом. Каждый раз при выборе плоскости нужно перебрать всевозможные границы примитивов по трем измерениям, вычислить в них значение функции стоимости и найти минимум среди всех этих значений. Когда мы вычисляем SAH для каждой плоскости, то нам необходимо знать N(left) и N(right) - количества примитивов справа и слева от плоскости. Если вычислять N простым перебором, в итоге получится квадратичный по сложности алгоритм построения.

Рисунок 3: Разбиние с учетом SAH

На рисунке 4 можно увидеть, что SAH сразу отбрасывает большие пустые пространства, плотно ограничивая геометрию.

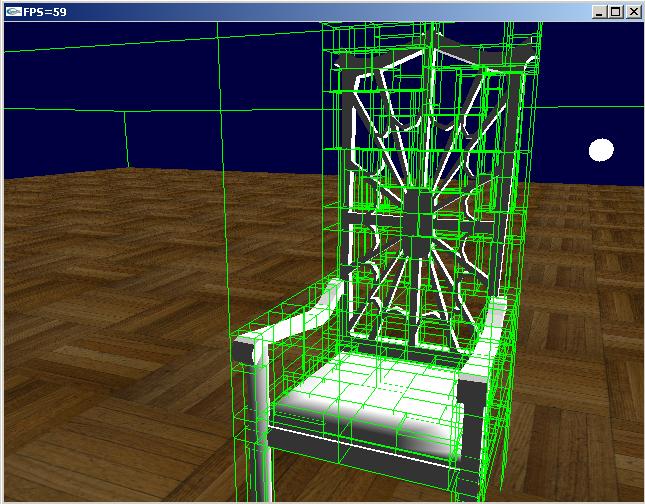
Рисунок 4: kd-дерево, построенное с учетом  SAH

Surface Area Heuristic порождает более интеллектуальный критерий остановки, чем предел глубины дерева или малое количество примитивов. Если для выбранной плоскости разбиения суммарная стоимость прослеживания дочерних узлов больше, чем стоимость прослеживания текущего узла как листа (то есть по формуле SurfaceArea(Node)*N(Node)), то посторение дерева следует остановить.

4. Быстрое построение kd дерева

Вариант 0

Разбивайте по центру, выбирая ось, по которой размер бокса максимален. Этот способ самый быстрый, но на некоторых сценах трассировка лучей в таком дереве примерно в 2-3 раза медленнее.

Вариант 1

Самое простое что можно сделать чтобы ускорить построение - это снизить количество перебираемых плоскостей. Вместо того, чтобы перебирать N плоскойстей (где N - количество примитивов), можно вычислить SAH лишь в небольшом числе заранее фиксированных мест. Входной бокс равномерно разбивается по каждой оси на M частей. Обычно M лежит в пределах от нескольких десятков до пары сотен. N(left) и N(right) попрежнему вычисляются перебором, но теперь нам придется сделать полный перебор по массиву всего лишь M раз, а не N. Таким образом, алгоритм приобретает сложность N*M. Фактически, мы достигли ускорения за счет огрубления SAH, дискретизовав ее. Однако оказывается, что значение минимума полученной грубой функции как правило не сильно отличается от ее точного минимума.

Вариант 2

Что можно сделать, чтобы ускорить вариант 1? Нужно избавиться от полного перебора во время вычисления N(left) и N(right). Для этого построим дерево, в каждом узле которого записана некоторая разбивающая плоскость и количество примитивов справа и слева от плоскости.

struct IntervalTree

{

    float split;

    int numPrimsOnLeftSide;

    int numPrimsOnRightSide;

На самом деле нам потребуется три таких дерева на каждом уровне - по одному на x,y,z. Входной интервал каждый раз будем делить пополам. Имея такое дерево, можно за log(N) операций достаточно точно определить количество примитивов справа и слева от плоскости. Алгоритм поиска в дереве выглядит достаточно просто.

vec2i IntervalTree::TraversePlane(float a_split) const

    if(a_split < split - EPSILON)

        if(left!=0)

            res += Left()->TraversePlane(a_split);

       //  если по какой-то причине количество примитивов равно нулю, то

        // посчитаем хотя бы те примитивы, которые есть в данном узле, чтобы SAH не занулялся.

        if(res.M[0] == 0)

    else if(a_split > split + EPSILON)

        if(right!=0)

        if(res[1] == 0)

    else

     } 

Сложность постоения дерева плоскостей - N*log(N). Сложность оценки SAH - M*log(N), так как мы вычисляем SAH только в M фиксированных плоскостях. Таким образом, суммарная сложность алгоритма - N*log(N), т.к. M много меньше N.

Перед тем как выполнять построение kd дерева можно впринципе построит произвольную ускоряющую структуру только для того, чтобы ускорить впоследствие вычисление SAH.

Вариант 3 (Почти точно и за N*Log(N))

Используем сортировку. Для каждой оси (x,y,z) отсортируем примитивы сначала по максимумам а затем по минимумам их ограничивающих боксов. Назовем массив, отсортированный по максимумам sorted_max. Массив, отсортированный по минимумам - sorted_min.

Проходя по массиву sorted_min слева напрваво, мы каждый раз в точности знаем сколько примитивов (вернее их ограничивающих боксов) лежит справа от плоскости (и почти точно знаем, сколько примитивов лежит слева). Проходя по массиву sorted_max справа налево мы точно знаем сколько примитивов лежит слева от плоскости и почти точно знаем, сколько лежит справа.

for(int axis = 0; axis < 3; axis++)

  // sort primitives belong to current axis and min bounds

  //

  CompareMin comparator(axis);

  std::sort(prims.begin(), prims.end(), comparator);

  for(int i=1;i<prims.size();i++)

    int onLeftSide = i;

    int onRightSide = prims.size()-i;

    float split = prims[i].Box().vmin[axis];

    if(split == a_box.vmin[axis])

      continue;

    // evaluate SAH

    AABB3f box_left = a_box;

    AABB3f box_right = a_box;

    box_left.vmax[axis] = split;

    box_right.vmin[axis] = split;

    float sah = EMPTY_COST + onLeftSide*SurfaceArea(box_left) + onRightSide*SurfaceArea(box_right);

    if (sah < min_sah)

      min_sah = sah;

      min_split = split;

      min_axis = axis;

  // sort primitives belong to current axis and max bounds

  //

  CompareMax comparator2(axis);

  std::sort(prims.begin(), prims.end(), comparator2);

  for(int i=prims.size()-2;i>=0;i--)

    int onLeftSide = i+1;

    int onRightSide = prims.size()-i-1;

    float split = prims[i].Box().vmax[axis];

    if(split == a_box.vmax[axis])

      continue;

    // evaluate SAH

    //

    AABB3f box_left = a_box;

    AABB3f box_right = a_box;

    box_left.vmax[axis] = split;

    box_right.vmin[axis] = split;

    float sah = EMPTY_COST + onLeftSide*SurfaceArea(box_left) + onRightSide*SurfaceArea(box_right);

    if (sah < min_sah)

      min_sah = sah;

      min_split = split;

      min_axis = axis;

В теории, у метода есть проблема. Рассмотрим массив sorted_min. Проходим по нему слева направо в цикле:

for (int i=0;i<prims.size();i++)

{

  int onLeftSide = i;

  int onRightSide = prims.size()-i;

  // ...

}

Число onLeftSide мы знаем абсолютно точно, а вот число onRightSide - не совсем. Дело в том, что плоскость может разбивать некоторые примитивы и в этом случае один и тот же примитив лежит как справа от плоскости, так и слева, что данный алгоритм не учитывает. На практике эта проблема практически себя не проявляет.

Вариант 4

Можно ускорить поиск минимума ф-ии SAH, использовуя како-нибудь метод минимизации с несколькими начальными приближениями. Скажем, метод золотого сечения. В данном случае мы так же избавляемся от метода полного перебора. Нужно только учитывать, что SAH приобретает более-менее гладкую форму только при большом числе примитивов. Плюс этого подхода в том, что вычисление SAH брутфорсом легко перекладывается на GPU. Поэтому оценивая каждый раз SAH грубой силой и сведя количество оценок к небольшому числу (~10-20 max), можно строить kd дерево таким методом очень быстро.

Вариант 5 (Binning)

    Часто используют именно этот вариант [2]. Ссуть состоит в следующем:

1. Нужно поделить пространство на регулярные интервалы по x,y и z. Каждый такой интервал называется корзиной (bin). Обычно ограничиваются небольшым числом корзин ~32.
2. Берутся центры треугольников и кладуться в корзины. Это означает что нужно пройтись по всем треугольникам, и вычислить их центры. После этого для каждой корзины нужно посчитать, сколько точек (центров) в нее попало. Это нетрудно сделать. При вычислении центра нужно просто увеличить соответствующий счетчик. Так как разбиение на корзины регулярно, имея координату точки, можно сразу же определить, в какую корзину она попадает. 
3. Далее нужно посчитать для всех границ корзин, сколько точек лежит справа от границы и сколько слева. Перебор плоскостей следует осуществлять на границах корзин.

Прослеживание луча в kd-дереве на CPU

Классический алгоритм бинарного поиска в kd деревьях (kd-tree traversal в англоязычной литературе), применяющийся в большинстве CPU реализаций, состоит примерно в следующем. На первом шаге алгоритма необходимо посчитать пересечение луча с ограничивающим сцену корневым параллелепипедом и запомнить информацию о пересечении в виде двух координат (в пространстве луча) – t_near и t_far, обозначающих пересечение с ближней и дальней плоскостями соответственно. На каждом следующем шаге необходима информация только о текущем узле (его адрес) и этих двух координатах.

При этом нет необходимости вычислять пересечение луча и дочернего параллелепипеда, достаточно лишь узнать пересечение с разбивающей параллелепипед плоскостью (обозначим соответствующую координату как t_split). Каждый нелистовой узел kd дерева имеет два дочерних узла. На рис. 5. изображены три варианта событий, которые могут возникать при прослеживании пути луча.

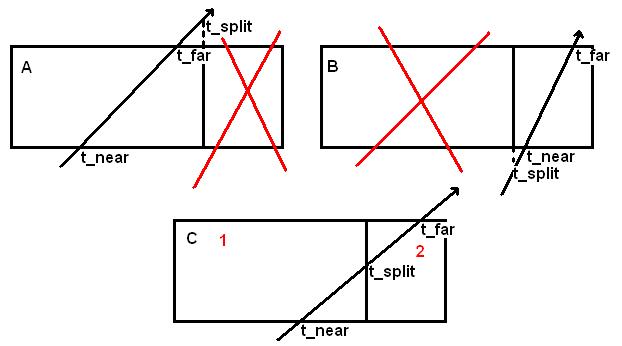
Рисунок 5: Прослеживание луча в kd дереве

В случае A (t_split >= t_far ) или B (t_split < t_near) луч пересекает только один дочерний узел, поэтому можно просто отбросить правый (соответственно левый) узел и продолжить поиск пересечения в оставшемся узле.

В случае C луч пересекает оба дочерних узла, поэтому необходимо сначала поискать пересечение в ближнем узле и если оно не найдено, искать его в дальнем. Так как в общем случае неизвестно, сколько раз произойдет последнее событие, необходим стек. Каждый раз, когда луч пересекает оба дочерних узла, адрес дальнего узла, t_near и t_far помещаются в стек и поиск продолжается в ближнем. Если в ближнем узле пересечение не найдено, из стека достаются адрес дальнего узла, t_near, t_far и поиск продолжается в дальнем узле.

Прослеживание луча в kd-дереве на GPU

Так как на GPU изначально отсутствует стек, появились бесстековые алгоритмы и алгоритмы, использующие искусственный стек небольшой длины. На GPU известны пять алгоритмов прослеживания пути луча -restart, backtrack, push-down, short stack и алгоритм прослеживания в kd дереве со связками.

kd-tree restart

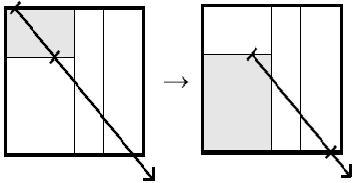
Рисунок 2:работа restart алгоритма.

Когда луч не находит пересечение в листе, его t_far приравнивается к t_near и поиск продолжается с корня kd-дерева (рис. 2). Грубо говоря, просто подвигается origin луча - то есть его точка испускания и поиск начинается сначала. Это приводит к тому, что луч проходит по одним и тем же узлам много раз, что неэффективно [3].

kd-tree push-down

Небольшая модификация restart алгоритма, заключающаяся в том, что луч стартует не с корня дерева, а с некоторого поддерева. Однако, в качестве нового поддерева узел может быть выбран, только если в течение всего спуска к нему не встретилось ни одного узла, в котором луч бы пересекал оба дочерних узла.

То есть, если при спуске по ближайшим узлам kd дерева хотя бы один раз встретился узел, в котором луч пересекает и ближний и дальний дочерние узлы, то именно этот дальний дочерний узел должен выть выбран в качестве поддерева. Далее, если луч промахнулся, рестарт будет произведен с запомненного дальнего узла и можно опять попытаться найти новое поддерево [4]. Фактически, это попытка завести стек длинной 1 элемент.

kd-tree short stack

Авторы [4] также использовали короткий стек. Пока размера стека хватает, идет его заполнение аналогично классическому алгоритму. Когда стек переполняется, он начинает работать как кольцевой буффер. Если стек пуст, необходимо произвести рестарт. Например, если в стеке длинной 4 содержаться узлы с номерами (1), (4), (6), (8), то при добавлении нового элемента (12), стек будет иметь следующий вид: (12), (4), (6), (8). То есть будет затерт первый элемент. Удаляться элементы будут в том порядке в каком они добавлялись (то есть сначала 12, потом 8, 6 и наконец 4), но когда из стека будет удален элемент (4), нужно будет произвести рестарт, так как мы затерли элемент (1). Смысл короткого стека в том, что он сильно сокращает количество restart-ов, которое приходится делать лучу.

kd-tree backtrack

Если сохранять в узлах kd дерева ссылку на родительские узлы, в случае промаха по этой ссылке можно добраться до родителя. Кроме того, потребуется хранить в каждом узле его ограничивающий паралеллипипид, чтобы иметь возможность вычислить новый t_far в случае промаха.

C t_near можно поступить так же, как и в случае restart алгоритма [3]. Это потребует дополнительно 6*4 (для координат паралеллипипида) + 4 (для ссылки на родителя) = 28 байт. Так как память на GPU довольно ограничена, такое расточительство может создать проблемы. К тому же, каждый раз при подъеме придется считать пересечение луча и выровненного по осям паралеллипипида, что конечно не бесплатно по вычислительным ресурсам. Следует особо отметить, что kd дерево с сохраненными паралеллипипид будет занимать намного больше памяти, чем хорошо построенное BVH дерево в этой же сцене. Основная причина здесь в том, что в kd дереве паралеллипипиды будут иметь больше общих точек, которые в итоге будут дублироваться.

kd-tree со связками

В этом варианте в каждый узел kd дерева добавляется шесть ссылок на соседние узлы дерева (те узлы, которые касаются данного узла) (рис. 3). Если луч промахнулся в текущем узле, то по связкам можно добраться до следующих узлов, в которых нужно прослеживать луч [5].

Этот алгоритм, как и backtrack позволяет избежать многократных прохождений по одним и тем же узлам дерева. Однако, шесть ссылок требуют дополнительно 24 байта памяти, что в сумме с имеющимися 8 дает 32 байта.

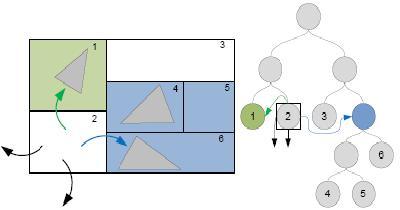
 Рисунок 3: kd дерево со связками.

Преимущества kd деревьев

1. Очень простой и эффективный алгоритм траверса. Даже для GPU.
2. Занимают мало памяти (8 байт на узел).

Недостатки kd деревьев

1. Трудоемкое построение, а именно, поиск разбиения с минимальным SAH.
2. Имеет большую глубину, чем BVH. Больше шагов при построении.

Заключение

Резюмируя, можно сказать, что kd дерево идеально для трасссировки лучей. Это верно как для CPU так и для GPU.

Литература

1. Wald I. Realtime Ray Tracing and Interactive Global Illumination. PhD thesis, Saarland University, 2004.

2. Shevtsov M., Soupikov A., Kapustin A. Highly Parallel Fast KD-tree Construction for Interactive Ray Tracing of Dynamic Scenes. In Proceedings of the EUROGRAPHICS conference, 2007.

3. Foley T., Sugerman J. KD-Tree Acceleration Structures for a GPU Raytracer. In Proceedings of the ACM SIGGRAPH/EUROGRAPHICS conference on Graphics hardware, p. 15-22, 2005.

4. Horn D., Sugerman J., Houston M., Hanrahan P. Interactive k-D Tree GPU Raytracing. Proceedings of the symposium on Interactive 3D graphics and games on Fast rendering, p. 167-174, 2007.

5. Popov S., Günther J., Seidel H.-P., Slusallek P. Stackless KD-Tree Traversal for High Performance GPU Ray Tracing. In Proceedings of the EUROGRAPHICS conference, 2007.